Post-Quantum Cryptography - Shor's Algorithm in Action

Introduction

Recently IBM released a free Practical introduction to quantum-safe cryptography course that helps "serves as a primer on the foundational concepts in quantum-safe cryptography". While the course itself I have been finding useful and do recommend, it reminded me of a previous Qiskit Event, Spring 2021, where I first practically experimented with Shor's algorithm. To my surprise, despite having the notebook uploaded to my personal repo I had not written up a summary of the event as I had done with previous ones.

This post will not only rectify the previous omission, but will serve as the kick off to a mini-series covering more in-depth Post-Quantum Cryptography. I want to start with this post, highlighting the fundamental reasons as to why we need PQC, explaining how Shor's algorithm threatens the underpinnings of our security premises today. A second post will cover the current efforts to introduce "Quantum-Safe Cryptography", covering loosely the mathematical concepts as well as standardization efforts currently underway with NIST. Lastly, I want to cover in a third post the experimentation and practical implementation of PQC in some of our day-to-day utilities. I took a look an initial look in March 2022 at experimental branches of SSH developed by Open Quantum Safe, however at the time I ended up choosing an algorithm that did not end up being selected by NIST. With some of the latest announcements by companies such as Signal announcing the latest PQC integration, I want to revisit those initial experiments and implement an iteration using some of the approaches selected by NIST.

Alright, enough planning, let's jump into learning how Shor's algorithm can break our current security!

Qiskit Event

As with previous Qiskit challenges, the Spring 2021 event was broken up into several notebooks with different focus areas. One of those, explored Shor’s algorithm, ultimately leading individuals to implementing a prime-factorization of the number 35. While this won’t directly allow us to break some of the modern day cryptography, since keys can be in the range of 2048-4096 bits, it demonstrates the inevitability that breaking the underpinning of our current security structures is no longer a theoretical possibility, it has moved to a problem of engineering. As quantum computers develop and get “better”, while at the same time more research is done expanding on Shor’s original implementation, it becomes a matter of “when”, not “if” current cryptographic implementations can be broken.

Before we jump too far down the rabbit hole let us go over the basics - Shor’s algorithm and covering the Qiskit notebook on how it was implemented practically.

Shor's Algorithm

As mentioned in the intro section, my corresponding notebook for the event can be found at my personal repo. What I would add on is that since the event some of the Qiskit documentation has changed with the site’s restructuring. If you follow the notebook and try to go to the Qiskit documentation for Shor’s it has changed to Shor’s Algorithm.

Algorithm Summary

Shor's algorithm ultimately solves the problem of period finding. This becomes important as factoring, the underpinning of current classical cryptography, can be turned into a period finding problem with polynomial time. This means if we can use Shor's to find an efficient way to find the period of $$f(x) = a^x\mod N$$ it can be used to find the prime factors used for encryption such as RSA.

What the Spring 2021 challenge had us implement was a quantum phase estimation of U, where the approach is $$U\left|y\right> = \left|ay\mod N\right>$$

Creating the Unitary

Since our challenge boils down to solve $$13y\mod 35$$ we already "know" how to solve this. We could mentally go through an iteration of multiples of 13 until we get back to our original state. In this case we can do it simply through classical confirmation, but the structure of how we setup this period is important, as we will be modelling it as a quantum unitary whose approach can be scaled where classically this becomes infeasible.

from qiskit import QuantumCircuit
from qiskit import QuantumRegister, QuantumCircuit
c = QuantumRegister(1, 'control')
t = QuantumRegister(2, 'target')
cu = QuantumCircuit(c, t, name="Controlled 13^x mod 35")

# WRITE YOUR CODE BETWEEN THESE LINES - START

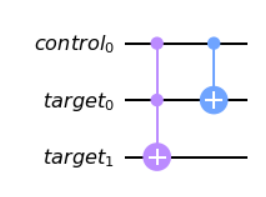
cu.ccx(c,t[0],t[1])
cu.cx(c,t[0])

Now with U complete, we can build out the remainder of the circuits needed. In this case we already know the period (r) is 4. This can be considered "cheating" as in a real example we would not know this ahead of time, however for this implementation we can proceed with the assumption the information is known. As a quick side-note since this mentally toyed with me during the challenge, there are references in the notebook itself for implementations with no assumption, showing that this particular implementation can be more efficient since we have some of the details already, however it is not mandatory to solve.

U2

c = QuantumRegister(1, 'control')
t = QuantumRegister(2, 'target')
cu2 = QuantumCircuit(c, t)

# WRITE YOUR CODE BETWEEN THESE LINES - START

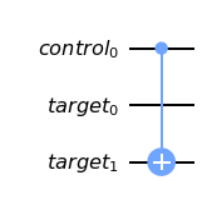
cu2.cx(c,t[1])

U4

Which in our case is a no-op, there is no change to the states therefore this unitary is “nothing”.

Final Circuit

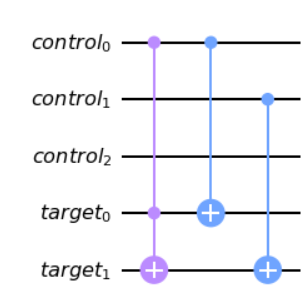
Putting all the components together, we get:

# Code to combine your previous solutions into your final submission
cqr = QuantumRegister(3, 'control')
tqr = QuantumRegister(2, 'target')
cux = QuantumCircuit(cqr, tqr)
solutions = [cu, cu2, cu4]
for i in range(3):
    cux = cux.compose(solutions[i], [cqr[i], tqr[0], tqr[1])
cux.draw('mpl')

Finding r

So we have a circuit. Great, what now? The total circuit will give us the output of s/r where r is the period of the original modulus function and s is a random integer between 0 and r-1.

from qiskit.circuit.library import QFT
from qiskit import ClassicalRegister
# Create the circuit object
cr = ClassicalRegister(3)
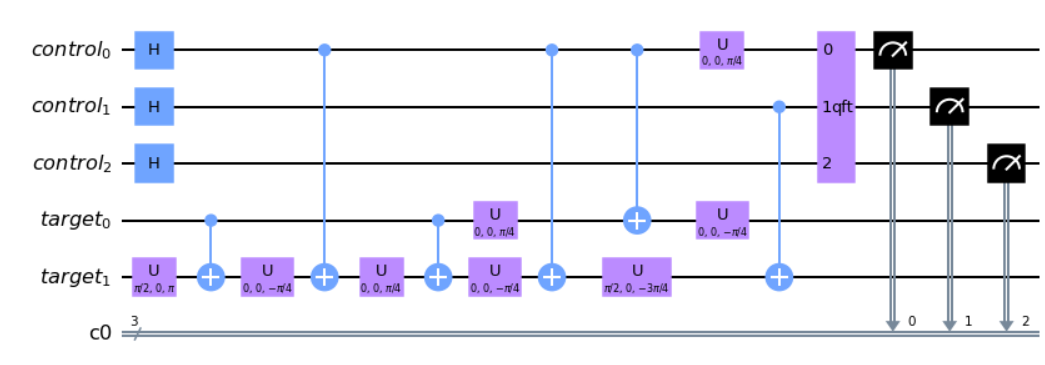
shor_circuit = QuantumCircuit(cqr, tqr, cr)

# Initialise the qubits
shor_circuit.h(cqr)

# Add your circuit
shor_circuit = shor_circuit.compose(cux)

# Perform the inverse QFT and extract the output
shor_circuit.append(QFT(3, inverse=True), cqr)
shor_circuit.measure(cqr, cr)
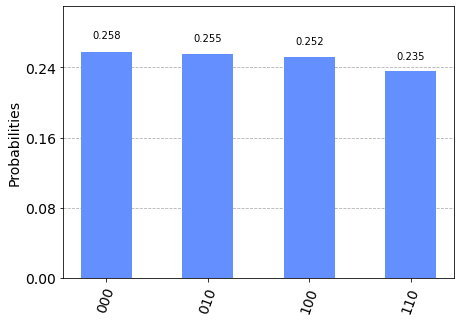
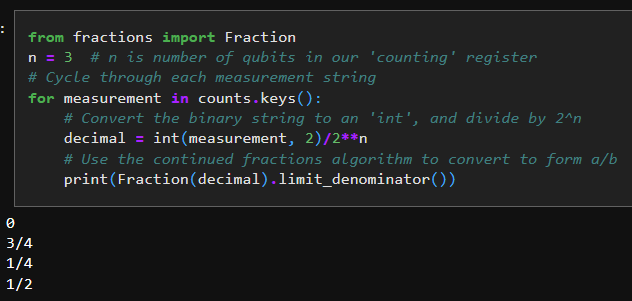
shor_circuit.draw('mpl')

Then running the circuit we get the results of 0,2,4,8.

But wait, didn't you say it should be giving us s/r? That doesn't seem to be the right numbers. There's one last part we didn't account for. The circuit itself is actually giving us $$2^n \cdot \frac{s}{r}$$ so we need to adjust appropriately.

And the 1/2 can be thought of as 2/4 here, giving us properly s/r with an r of 4. Now, again, we knew this ahead of time because we cheated by doing it mentally first. But this illustrates that the circuit can get us a proper answer, which is the main point of going through the steps to generate the circuit and confirm the output.

Getting the factors of 35

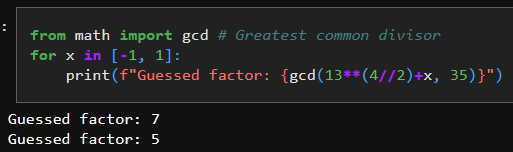
So how do we get the factors from r? There is a high chance that at least one of the greatest common divisor between N (in our case 35) and either $$a^\frac{r}{2}-1$$ or $$a^\frac{r}{2}+1$$ is a factor of N. Since GCD is easily computed classically we can find that as:

In this case it's easy to see that both ended up being the factors of 35, however were only one of them a true factor, then finding the other would simply be dividing N by the factor found. Congratulations, you just factored a number using Shor's approach!

Summary

I was debating including the following "simplified" approach to Shor's earlier in the post, but I felt that including this now, after you've gone through the practical implementation should allow for deeper understanding. The mathematical explanation comes from the latest Developer course on Post-Quantum Cryptography listed in the introduction, and I highly suggest going through that to reinforce the concepts seen here as well as provide different implementation overviews.

Hopefully this walkthrough helped cut through the underlying explanation of how Shor's algorithm provides a threat to the current classical approach to our security processes. What we will cover in a next post is the answer to Shor's - how the industry is evolving to address security in a "quantum-safe" approach, and the standardization efforts around it. We are the latest precipice of security and computing paradigms and learning more about both the threats and future approaches is fundamental to ensure we are keeping our environments safe. It is never too early to start learning and not only be ready for what comes next, but to be able to help shape it as well.

Thanks folks, until next time!