Home Post-Quantum Cryptography - Practical Kyber Experimentation
Post
Cancel

Post-Quantum Cryptography - Practical Kyber Experimentation

Posted Oct 7, 2023 Updated Oct 10, 2023
By Patrick Downing
12 min read

Introduction

At this point we’ve gone through how Shor’s algorithm can be used to break the fundamental difficulty assumptions of our current security paradigms. Additionally, we’ve looked at NIST’s PQC Standardization efforts and how the industry is trying to address this shift in security fundamentals. In this third post we will continue down that rabbit hole exploring the Kyber system more closely, taking a second look at the underlying math specific to Kyber 512, comparing that to experimental branches provided by Open Quantum Safe, and then implementing it to communicate between two different machines on my lab environment using a hybrid-PQC approach.

The importance at the moment in my mind is less about the specific implementation used and more about understanding the migration journey. That might be a contentious point but I’ll step through my thinking. Industry members are approaching their own PQC journeys differently. Recently Signal announced it’s pqxdh Key Agreement Protocol which leverages Crystals-Kyber-1024 as its Key Encapsulation Mechanism (KEM). Similarly, Google is rolling out a hybrid Kyber768-based KEM in Chrome to start its own PQC journey. Different approaches, however this is just two examples of companies/products starting to roll out variations.

Now, where is the contentious point? You might say both are using different iterations flavours of Kyber, but are staying within the bounds of NIST guidelines. You would essentially be right, however while the standardization efforts are ongoing there are different security claims refuting NIST’s findings on Kyber. If these claims are true, then the security of Kyber is not as strong as NIST is claiming. This is not to say that Kyber is not secure, but rather that the jury is still out on the security of Kyber, so it’s important to understand the migration journey and not just the specific implementation.

Time will tell which approaches end up on top. That is why I say, at the moment at least, understanding how to migrate becomes more important than the specific flavour you are using. Understanding the current offerings, limitations, and having a plan on how to migrate, will become algorithm-agnostic.

With that said, I did want to spend the rest of the time on this post diving into Kyber. While there are open questions as far as the security offered by Kyber 512, it allows a good base to look at the math, code, and practical implementation. The lessons learned through this experimentation will be useful even if I wanted to use a different, non-Kyber, approach in the future, and helps prepare me for what may come.

Let’s dive in!

Kyber Specifics

Kyber at its heart is a public-key encryption system working with vectors of polynomials, otherwise known as Module Learning with Errors (MLWE), which we covered in the previous post. This means we will be working with public and private keys as well as modulo. Since we are working with vectors of polynomials, we need both a modulus for numbers, q as well as a modulus for polynomials, f, to ensure that the degree of polynomials doesn’t grow too large to handle.

I’ll cover the Kyber process here, but I’ll add in that if you want to go through a “baby-Kyber” example that encrypts and decrypts the number 11, I highly suggest reading through Approachable Cryptography’s post on Kyber which concretely covers each step with a practical demonstration.

The main difference on the various implementations of Kyber are on the parameters and compression. For the sake of what we will be covering practically later, let’s focus on Kyber 512 at the moment. First, let’s baseline the parameters.

maximum degree of the used polynomial: \(n = 256\)
number of polynomials per vector: \(k = 2\)
modulus for numbers: \(q = 3329\)
how big the coefficients of the "small" polynomials can be: \(η_{1}=3, η_{2}=2\)

The private key s is a vector of small polynomials. An example based on parameters above:

$$s = (3x^{256} -2x^{255} \dots + x + 2, -2x^{256} - 3x^{255} \dots - x - 2)$$

The public key is two elements; a matrix A of random polynomials, who’s coefficients are taken modulo q, and a vector polynomial t, which to calculate we also need an error vector e which consists of small coefficient polynomials similar to s.

$$A = \begin{pmatrix}3328x^{256} -569x^{255} \dots + 3001x + 2407 & - 157x^{256} - 726x^{255} \dots - 3209x - 2300 \\\ 156^{256} -386x^{255} \dots + 2438x + 1679 & -1920x^{256} - 502x^{255} \dots - 2610x - 152\end{pmatrix}$$

$$e = (3x^{256} +x^{255} \dots - 2x + 1, -2x^{256} - x^{255} \dots + 3x - 1)$$

We can then calculate the polynomial vector t as:

$$t = As + e$$

At which point we have our keys:

  • Private key: s
  • Public key: (A,t)

For the encryption and decryption portions I will again highly suggest going through the Approachable Cryptography’s mini-Kyber example as it keeps the parameters low to keep the calculations understandable. The fun part of this as mentioned is that the implementation of Kyber is generally the same and the fundamental differences are in the parameters chosen. Having set the base above with Kyber 512, we can now take a look at some experimental branches and compare to our theoretic understanding.

Open Quantum Safe

The Open Quantum Safe team has open-sourced a C library which implements most of the PQC algorithms, including Kyber - liboqs. Our goal will be to leverage OQS’s openssh repo, however that is ultimately leveraging liboqs for the PQC portions, so let’s start there.

Kyber Code

Let’s take a look at the Kyber 512 implementation and see if we recognize some of the details.

At the Kyber 512 params.h file we see some familiar parameters:

#if   (KYBER_K == 2)
#define KYBER_NAMESPACE(s) pqcrystals_kyber512_ref_##s
...
#define KYBER_N 256
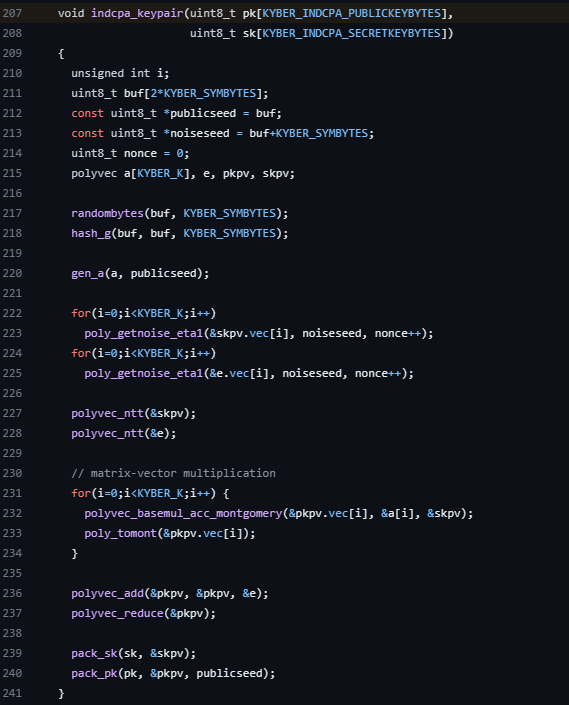
#define KYBER_Q 3329

Well that looks like something we’ve seen doesn’t it! Without going through the code completely, we can dive a few levels from the kem.c file to the indcpa.c file where we start to see some more familiar math happening - the keypair generation!

There is a little to unpack here, so let’s go one step by step and compare it to the mathematical implementation we did above.

First thing first, we understand these polynomial vectors being defined:

polyvec a[KYBER_K], e, pkpv, skpv;

a maps to our A, e maps to e. The secret key, s above, maps to skpv, and our public key t above maps to pkpv. Great so far so good.

gen_a(a, publicseed);

All this is doing is populating the matrix A.

  for(i=0;i<KYBER_K;i++)
    poly_getnoise_eta1(&skpv.vec[i], noiseseed, nonce++);
  for(i=0;i<KYBER_K;i++)
    poly_getnoise_eta1(&e.vec[i], noiseseed, nonce++);

  polyvec_ntt(&skpv);
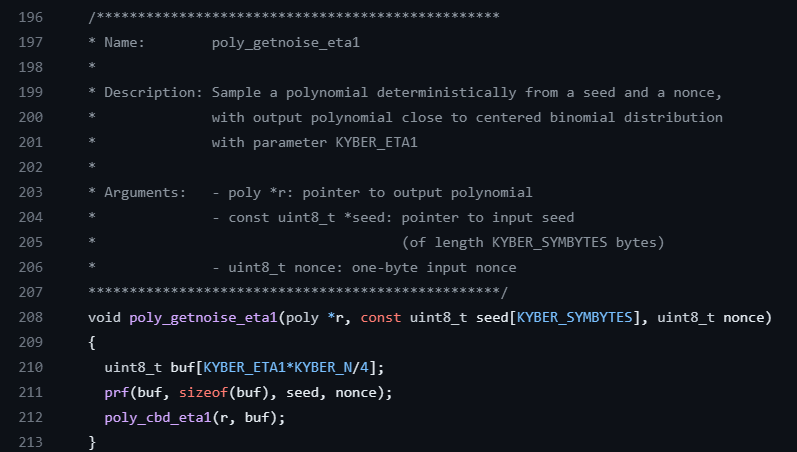
  polyvec_ntt(&e);

Since our secret key s and error vector e are generated similarly, this part of the code is reusing the same function to populate them. Here it’s worth poking one layer deeper at the poly_getnoise_eta1 function for a moment to highlight one more parallel to our mathematical walkthrough above. This function is located in the poly.c file.

Where KYBER_ETA1 here matches \(η_{1}=3\) as we saw above for Kyber 512!

The rest of the code back in indcpa.c is calculating \(t = As + e\), where the first part is the multiplication:

  // matrix-vector multiplication
  for(i=0;i<KYBER_K;i++) {
    polyvec_basemul_acc_montgomery(&pkpv.vec[i], &a[i], &skpv);
    poly_tomont(&pkpv.vec[i]);
  }

Then adding our error vector:

  polyvec_add(&pkpv, &pkpv, &e);
  polyvec_reduce(&pkpv);

See, that wasn’t too bad!

Alright, we have a decent understanding of what is happening now. So let’s go move away from theory & code and move on to getting our hands dirty with implementation!

Installing & Configuration

The goal was to install OQS’s openssh on both my laptop and a pi, and be able to communicate between the two. A fun-fact I was originally looking to use a spare pi 3B, however when going through the builds I kept running into out of memory situations. I dusted off one of my org-in-a-box’s pi 4s and thankfully it was able to successfully build the libraries.

Hardware limitations aside, the actual build process couldn’t have been simpler. Cloning the openssh repo, there are scripts to help build the required liboqs libraries, then build the openssh binary with the PQC support.

./oqs-scripts/clone_liboqs.sh
./oqs-scripts/build_liboqs.sh
./oqs-scripts/build_openssh.sh

I was just following the instructions in the repo and ended up generating all the valid keypairs. This could have been limited to just what was needed for our experiment, however there was no harm, other than waiting several minutes for the full suite to finish.

make tests -e LTESTS=""

Once the build was complete on both laptop/pi I updated my ~/openssh/regress/sshd_config file on the pi (acting as server) to allow connections from more than just localhost (which is the default for the OQS experimental branch. It’s experimental for a reason after all!):

ListenAddress           0.0.0.0

I then updated my ~/openssh/regress/ssh_config on the laptop (acting as client) to limit the amount of Identity files to only the Sphincs Identity generated directly. Since I was limiting myself to NIST suggested algorithms, I decided to use Sphincs together with Kyber for the SSH authentication.

./ssh-keygen -t ssh-ecdsa-nistp521-sphincssha2256fsimple -f ~/ssh_client/id_ssh-ecdsa-nistp521-sphincssha2256fsimple

Leveraging the following in the ssh_config.

IdentityFile /home/padraignix/ssh_client/id_ssh-ecdsa-nistp521-sphincssha2256fsimple

This section wasn’t strictly necessary since it was defined in the command line arguments, however I found that with the default full list of IdentityFile’s in the config I was running into auth failures. After cleaning up the config to only include the Sphincs Identity, I was able to successfully authenticate.

And with that, we should be all set to go! Let’s give it a shot!

Post-Quantum Communication!

First thing we need to do is kick off the server to listen for incoming connections. From the pi:

padraignix@pqc:~/openssh$ /home/padraignix/openssh/sshd -D -f regress/sshd_config -o KexAlgorithms=ecdh-nistp256-kyber-512r3-sha256-d00@openquantumsafe.org -o HostKeyAlgorithms=ssh-ecdsa-nistp521-sphincssha2256fsimple -o PubkeyAcceptedKeyTypes=ssh-ecdsa-nistp521-sphincssha2256fsimple -h regress/host.ssh-ecdsa-nistp521-sphincssha2256fsimple

Then from my laptop I tried to connect to the pi:

padraignix:~/openssh$ /home/padraignix/openssh/ssh -o KexAlgorithms=,ecdh-nistp256-kyber-512r3-sha256-d00@openquantumsafe.org -o HostKeyAlgorithms=ssh-ecdsa-nistp521-sphincssha2256fsimple -o PubkeyAcceptedKeyTypes=ssh-ecdsa-nistp521-sphincssha2256fsimple -o PasswordAuthentication=no -i ~/ssh_client/id_ssh-ecdsa-nistp521-sphincssha2256fsimple 10.0.0.23 -p 4242 -vvv

I added all the debugging to be able to confirm the use of our PQC algorithms, as well as tailing the /var/log/auth.log on the pi to see the connection attempts.

Behold the live capture of the attempt!

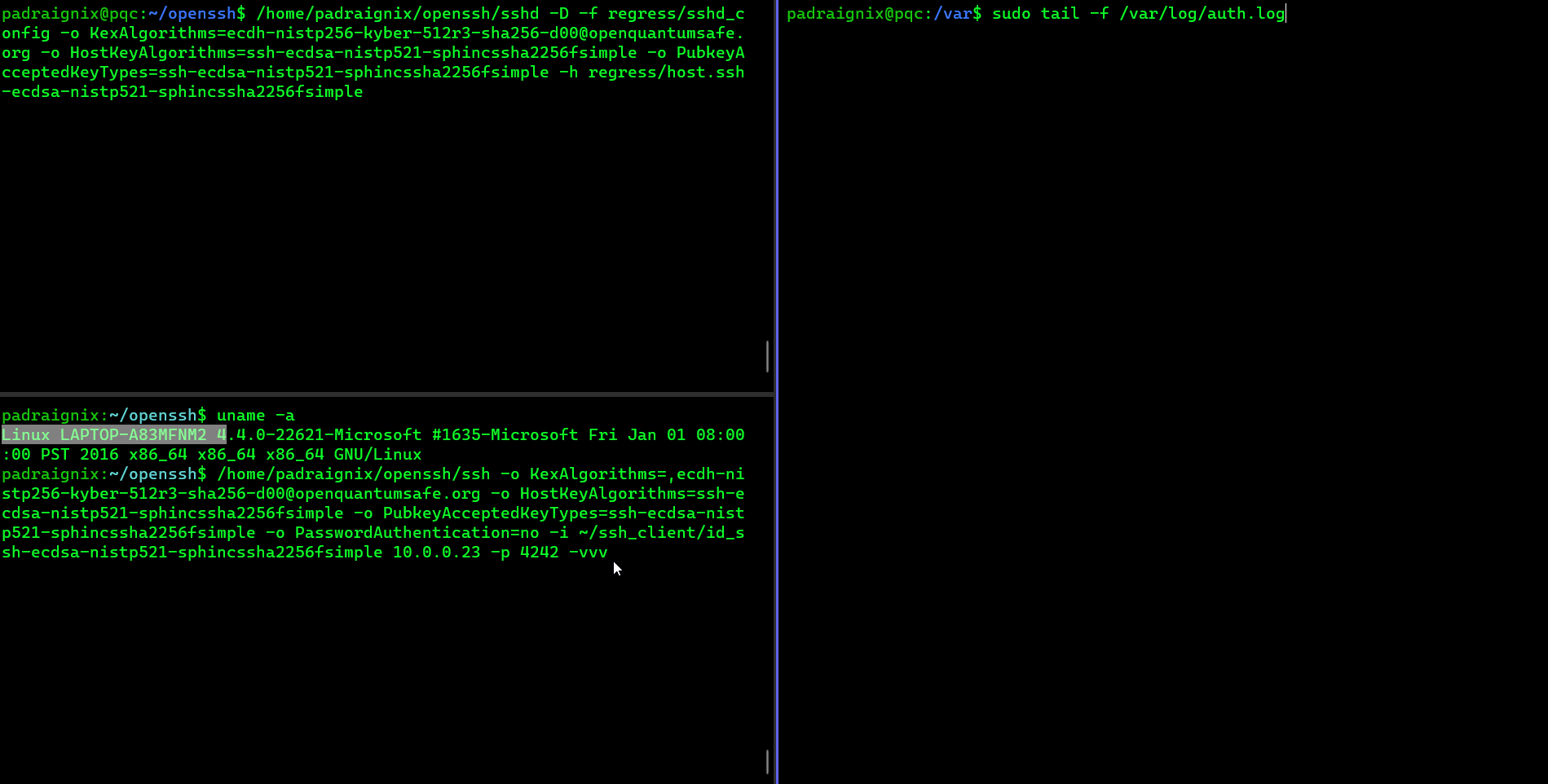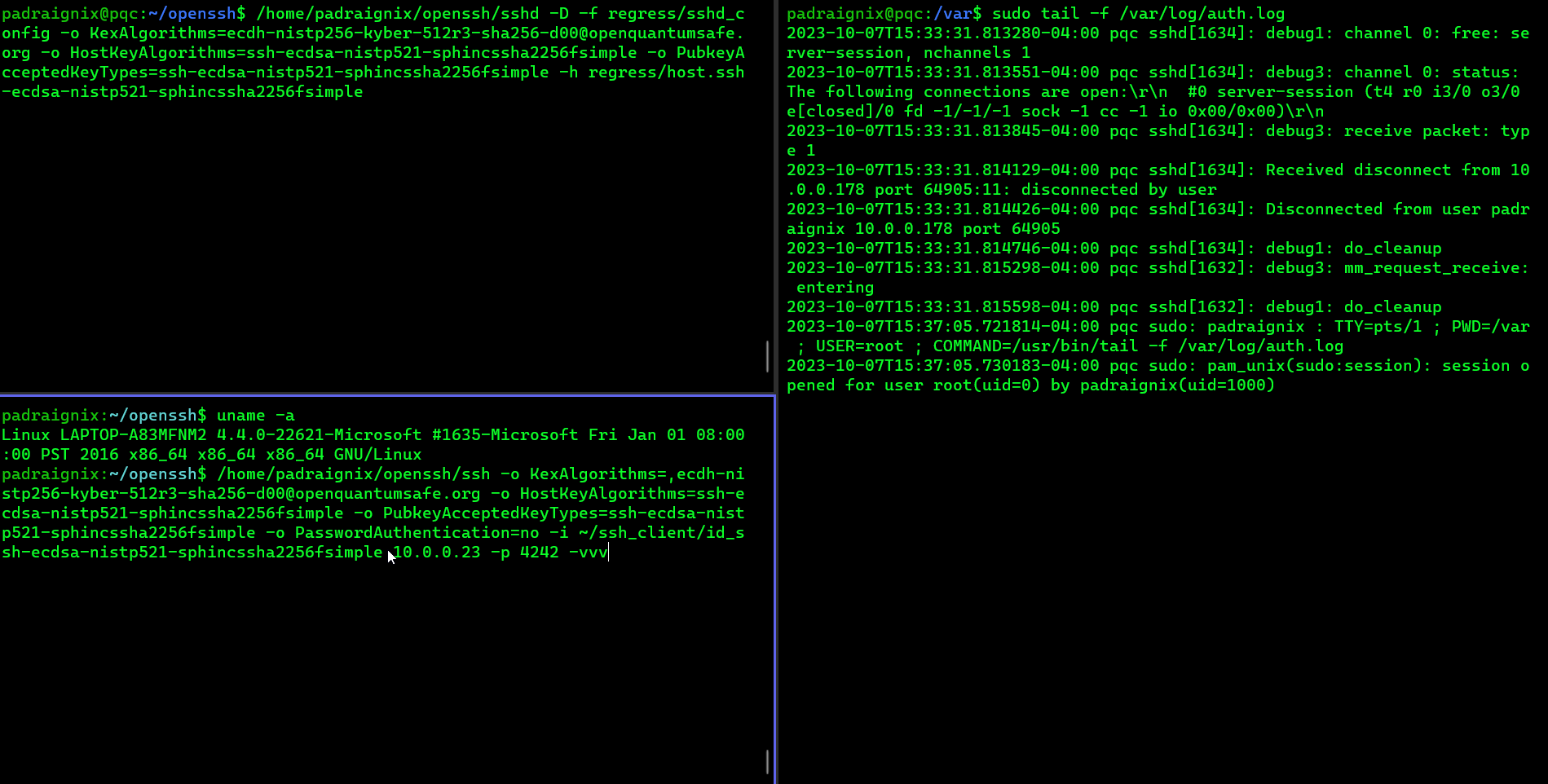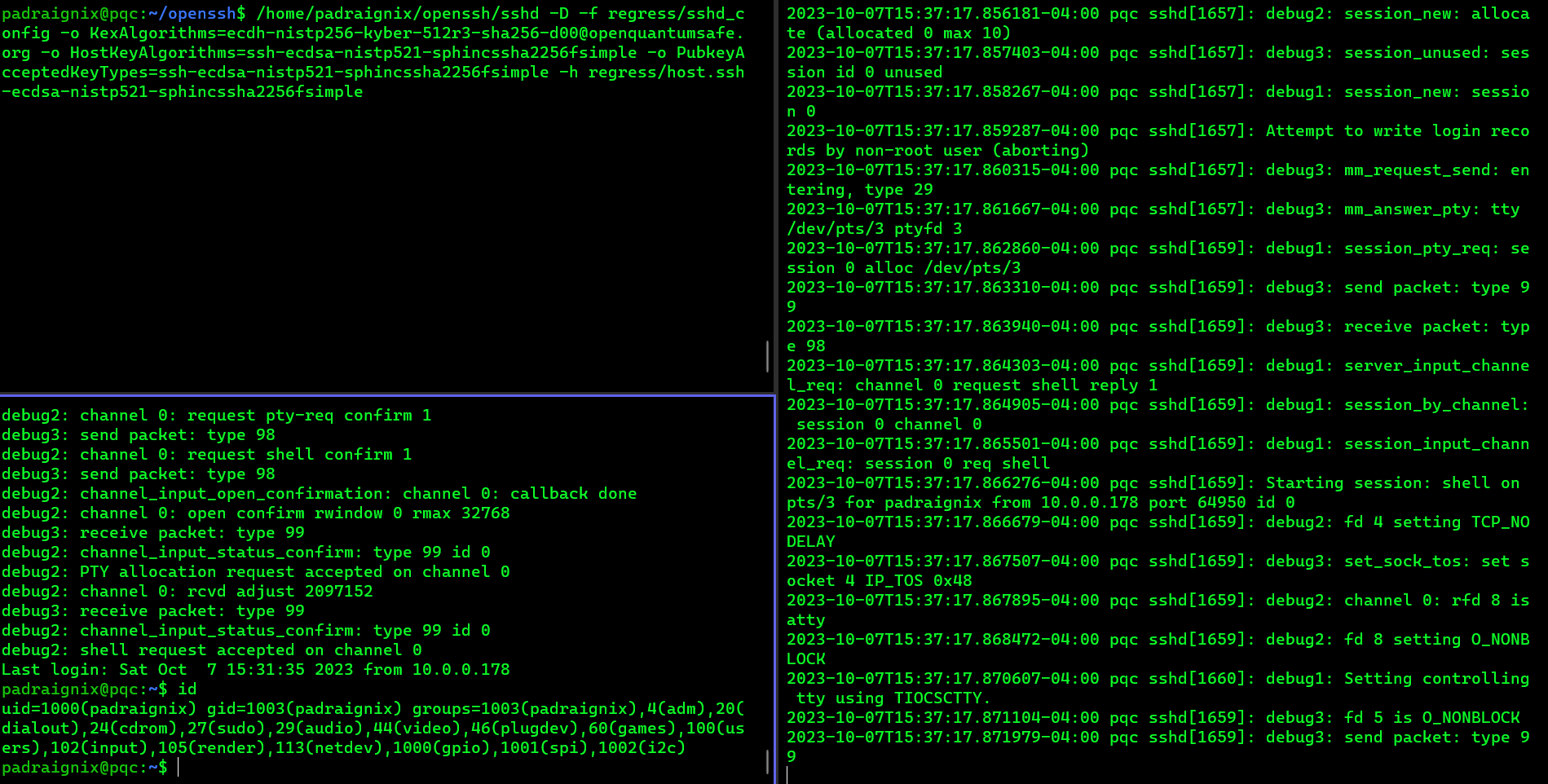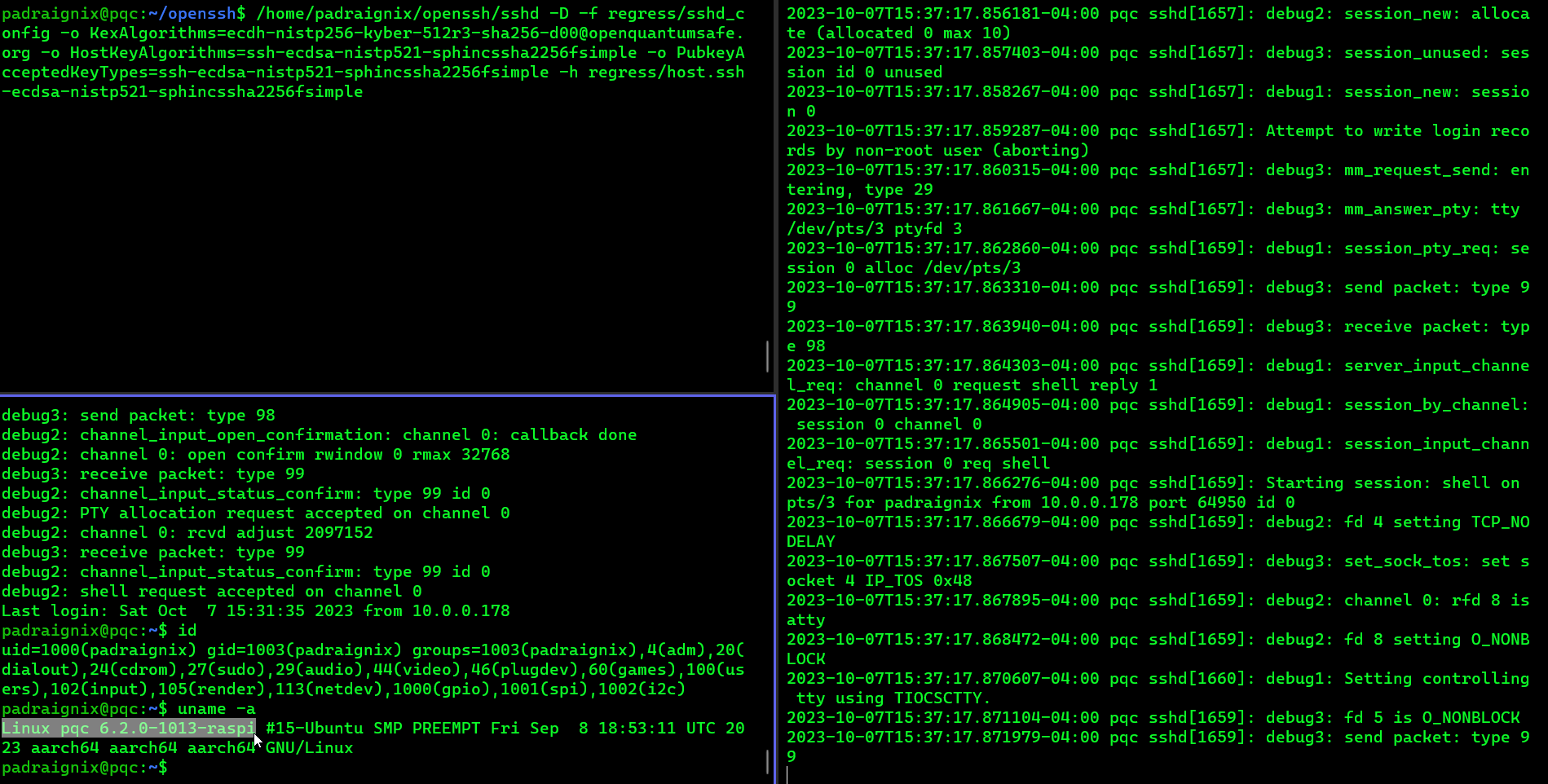
Success! We have a post-quantum SSH connection! Or… we should, let’s confirm based on the logs at least. From the client side we see:

debug2: local client KEXINIT proposal
debug2: KEX algorithms: ecdh-nistp256-kyber-512r3-sha256-d00@openquantumsafe.org,ext-info-c
debug2: host key algorithms: ssh-ecdsa-nistp521-sphincssha2256fsimple
...
debug2: peer server KEXINIT proposal
debug2: KEX algorithms: ecdh-nistp256-kyber-512r3-sha256-d00@openquantumsafe.org
debug2: host key algorithms: ssh-ecdsa-nistp521-sphincssha2256fsimple
...
debug1: kex: algorithm: ecdh-nistp256-kyber-512r3-sha256-d00@openquantumsafe.org
debug1: kex: host key algorithm: ssh-ecdsa-nistp521-sphincssha2256fsimple
debug3: send packet: type 30
debug1: expecting SSH2_MSG_KEX_ECDH_REPLY
debug3: receive packet: type 31
debug1: SSH2_MSG_KEX_ECDH_REPLY received
debug1: Server host key: ssh-ecdsa-nistp521-sphincssha2256fsimple SHA256:p70cP2NYYQnsMDJCbCUQT6Yapkc8UXx1RLlP/Sf1uL8
debug3: record_hostkey: found key type ECDSA_NISTP521_SPHINCSSHA2256FSIMPLE in file /home/padraignix/.ssh/known_hosts:5
...
debug1: Will attempt key: /home/padraignix/ssh_client/id_ssh-ecdsa-nistp521-sphincssha2256fsimple ECDSA_NISTP521_SPHINCSSHA2256FSIMPLE SHA256:Sk6FBYZPQO1N35xkAr2y+En2QViQXwFbEaxoIZN7St8 explicit
debug1: Offering public key: /home/padraignix/ssh_client/id_ssh-ecdsa-nistp521-sphincssha2256fsimple ECDSA_NISTP521_SPHINCSSHA2256FSIMPLE SHA256:Sk6FBYZPQO1N35xkAr2y+En2QViQXwFbEaxoIZN7St8 explicit
debug1: Server accepts key: /home/padraignix/ssh_client/id_ssh-ecdsa-nistp521-sphincssha2256fsimple ECDSA_NISTP521_SPHINCSSHA2256FSIMPLE SHA256:Sk6FBYZPQO1N35xkAr2y+En2QViQXwFbEaxoIZN7St8 explicit
...
debug3: sign_and_send_pubkey: signing using ssh-ecdsa-nistp521-sphincssha2256fsimple SHA256:Sk6FBYZPQO1N35xkAr2y+En2QViQXwFbEaxoIZN7St8
Enter passphrase for key '/home/padraignix/ssh_client/id_ssh-ecdsa-nistp521-sphincssha2256fsimple':
debug3: send packet: type 50
debug3: receive packet: type 52
Authenticated to 10.0.0.23 ([10.0.0.23]:4242) using "publickey".

Excellent, now let’s check the server side logs:

2023-10-07T15:37:14.026456-04:00 pqc sshd[1657]: Connection from 10.0.0.178 port 64950 on 10.0.0.23 port 4242 rdomain ""
2023-10-07T15:37:14.046402-04:00 pqc sshd[1657]: debug1: list_hostkey_types: ssh-ecdsa-nistp521-sphincssha2256fsimple [preauth]
2023-10-07T15:37:14.046877-04:00 pqc sshd[1657]: debug3: send packet: type 20 [preauth]
2023-10-07T15:37:14.047449-04:00 pqc sshd[1657]: debug1: SSH2_MSG_KEXINIT sent [preauth]
2023-10-07T15:37:14.047894-04:00 pqc sshd[1657]: debug3: receive packet: type 20 [preauth]
2023-10-07T15:37:14.048444-04:00 pqc sshd[1657]: debug1: SSH2_MSG_KEXINIT received [preauth]
2023-10-07T15:37:14.048901-04:00 pqc sshd[1657]: debug2: local server KEXINIT proposal [preauth]
2023-10-07T15:37:14.049491-04:00 pqc sshd[1657]: debug2: KEX algorithms: ecdh-nistp256-kyber-512r3-sha256-d00@openquantumsafe.org [preauth]
2023-10-07T15:37:14.049877-04:00 pqc sshd[1657]: debug2: host key algorithms: ssh-ecdsa-nistp521-sphincssha2256fsimple [preauth]
...
2023-10-07T15:37:14.054328-04:00 pqc sshd[1657]: debug2: KEX algorithms: ecdh-nistp256-kyber-512r3-sha256-d00@openquantumsafe.org,ext-info-c [preauth]
2023-10-07T15:37:14.055095-04:00 pqc sshd[1657]: debug2: host key algorithms: ssh-ecdsa-nistp521-sphincssha2256fsimple [preauth]
...
2023-10-07T15:37:14.060117-04:00 pqc sshd[1657]: debug1: expecting SSH2_MSG_KEX_ECDH_INIT [preauth]
2023-10-07T15:37:14.063062-04:00 pqc sshd[1657]: debug3: receive packet: type 30 [preauth]
2023-10-07T15:37:14.063474-04:00 pqc sshd[1657]: debug1: SSH2_MSG_KEX_ECDH_INIT received [preauth]
2023-10-07T15:37:14.064187-04:00 pqc sshd[1657]: debug3: mm_sshkey_sign: entering [preauth]
2023-10-07T15:37:14.064566-04:00 pqc sshd[1657]: debug3: mm_request_send: entering, type 6 [preauth]
2023-10-07T15:37:14.064910-04:00 pqc sshd[1657]: debug3: mm_sshkey_sign: waiting for MONITOR_ANS_SIGN [preauth]
2023-10-07T15:37:14.065191-04:00 pqc sshd[1657]: debug3: mm_request_receive_expect: entering, type 7 [preauth]
2023-10-07T15:37:14.065488-04:00 pqc sshd[1657]: debug3: mm_request_receive: entering [preauth]
2023-10-07T15:37:14.065822-04:00 pqc sshd[1657]: debug3: mm_request_receive: entering
2023-10-07T15:37:14.066158-04:00 pqc sshd[1657]: debug3: monitor_read: checking request 6
2023-10-07T15:37:14.066441-04:00 pqc sshd[1657]: debug3: mm_answer_sign: entering
2023-10-07T15:37:14.580369-04:00 pqc sshd[1657]: debug3: mm_answer_sign: ssh-ecdsa-nistp521-sphincssha2256fsimple KEX signature len=50085
...
2023-10-07T15:37:14.653374-04:00 pqc sshd[1657]: debug1: userauth-request for user padraignix service ssh-connection method publickey [preauth]
2023-10-07T15:37:14.655504-04:00 pqc sshd[1657]: debug2: userauth_pubkey: valid user padraignix querying public key ssh-ecdsa-nistp521-sphincssha2256fsimple AAAAKHNzaC1lY2RzYS1uaXN0cDUyMS1zcGhpbmNzc2hhMjI1NmZzaW1wbGUAAAAIbmlzdHA1MjEAAACFBAGnsXjuFqEkkb7FsyOISt8ZKJQxM9jEB/nc2FfLopdq3oCtXG/NcFtesxhXoUyr8VPthx/AIzt4HdGIFNAMXTD02wG/CUQ5s4KDBEuLv42x4tvcKYXTO7rk8VL7BKlNc+Y8/1po9XFNRgwsvHXfe3GwO4JLExP99a7TUGN50dV51jYFigAAAEBtoj7VNwfqkxjRJHDKnmd1biP/tqBYYHa23awFQGtSnSIGef+7xR1Umg9oFIaL1D11G77rDHJkNBMk8b/1WM4y [preauth]
2023-10-07T15:37:14.672766-04:00 pqc sshd[1657]: debug1: userauth_pubkey: publickey test pkalg ssh-ecdsa-nistp521-sphincssha2256fsimple pkblob ECDSA_NISTP521_SPHINCSSHA2256FSIMPLE SHA256:Sk6FBYZPQO1N35xkAr2y+En2QViQXwFbEaxoIZN7St8 [preauth]
2023-10-07T15:37:14.673136-04:00 pqc sshd[1657]: debug3: mm_key_allowed: entering [preauth]
...
2023-10-07T15:37:14.685445-04:00 pqc sshd[1657]: debug1: trying public key file /home/padraignix/openssh/regress/authorized_keys_padraignix
2023-10-07T15:37:14.704629-04:00 pqc sshd[1657]: debug1: /home/padraignix/openssh/regress/authorized_keys_padraignix:2: matching key found: ECDSA_NISTP521_SPHINCSSHA2256FSIMPLE SHA256:Sk6FBYZPQO1N35xkAr2y+En2QViQXwFbEaxoIZN7St8
2023-10-07T15:37:14.705466-04:00 pqc sshd[1657]: Accepted key ECDSA_NISTP521_SPHINCSSHA2256FSIMPLE SHA256:Sk6FBYZPQO1N35xkAr2y+En2QViQXwFbEaxoIZN7St8 found at /home/padraignix/openssh/regress/authorized_keys_padraignix:2
...
2023-10-07T15:37:17.703922-04:00 pqc sshd[1657]: Accepted publickey for padraignix from 10.0.0.178 port 64950 ssh2: ECDSA_NISTP521_SPHINCSSHA2256FSIMPLE SHA256:Sk6FBYZPQO1N35xkAr2y+En2QViQXwFbEaxoIZN7St8

There we go. Successful PQC connection between my two machines. I’ll take it!

Summary & Future Analysis

What a journey. We went from the original posts of understanding Shor’s algorithm’s threat to current encryption approaches, to understanding the industry’s response and standardization efforts to address this, to ultimately in this post looking at the math behind Kyber, comparing it to the experimental code, and implementing it in a practical way.

There are many more things to explore, such as performance comparisons to undertand migration questions at scale, but I think this is a good stopping point for now. Considering this area is very much still a work in progress and there are open questions and efforts on what will ultimately be the standardized algorithms, I’m sure I’ll revisit this in the future, but for now I’m happy with the results.

Going back to one of my original points, understanding how to migrate becomes more important than the specific flavour you are using. Understanding the current offerings, limitations, and having a plan on how to migrate, will pay dividends, now, where should things change (and chances are they will), we can be ready to understand and adapt.

Thanks folks, until next time!

quantum-computing
quantum cryptography post-quantum cryptography lattice based crypto
This post is licensed under CC BY 4.0 by the author.
Recently Updated
Contents