Introduction

For the final week of IBM's Quantum Challenge Fall 2020 we had to put the Grover and qRAM experience we had gained in the first two weeks to the test. Using the knowledge we had developed we were provided with a new "Asteroid Clearing" problem which ended up being similar to the classical n-queens problem.

Apart from solving the problem solely using Quantum Circuits, a veritable feat in itself, the competitive nature of this challenge was in continuously optimizing the cost of your circuit to the lowest possible configuration while still ensuring the circuit solves the full problem space.

This post will cover a few different aspects. Initially it will cover my theoretical solution and corresponding circuit. Afterwards I will cover each improvement iteration, what I targetted and implemented in the improvement, and the subsequent lowered score. The final improvement section will also cover qSphere diagram flows to help elaborate on the theory leveraged.

This walkthrough is less about using Grover's in any specifically special manner, in fact I have some questions and doubts about the final implementation based on empirical evidence gathered through this challenge that I will highlight in the final section. The focus is really the journey from an initial solution, then how without structurally changing the overall flow repeating iterations until I reached a circuit complexity of only 10% the original solution. All while still solving the same original problem space.

The Qiskit team's challenge notebook can be found on their Github Page. Without further delay, let's jump into the challenge!

Challenge Problem Statement

The problem statement started with our favourite Dr. Ryoko stuck in the multiverse with a quick description of what would end up being the challenge we need to solve.

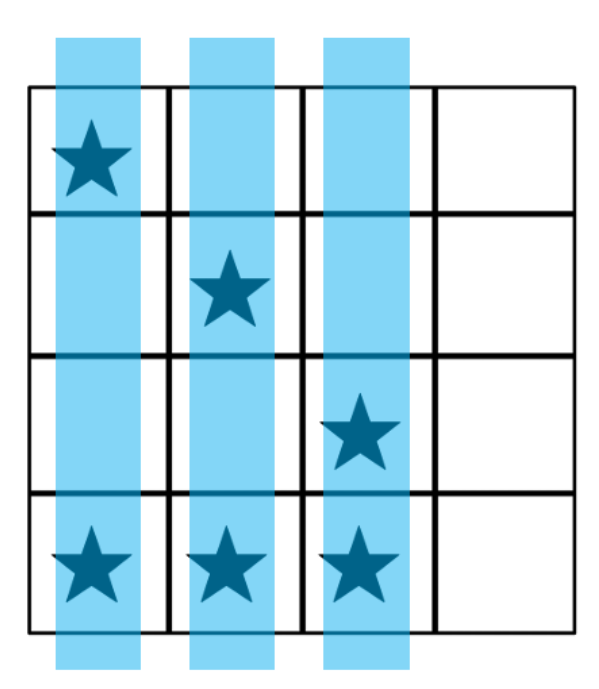
We were provided an example that illustrates the problem space in terms of asteroids on a 4x4 board.

Subsequently we were also provided an example of how a board could be solvable with three laser beam shots.

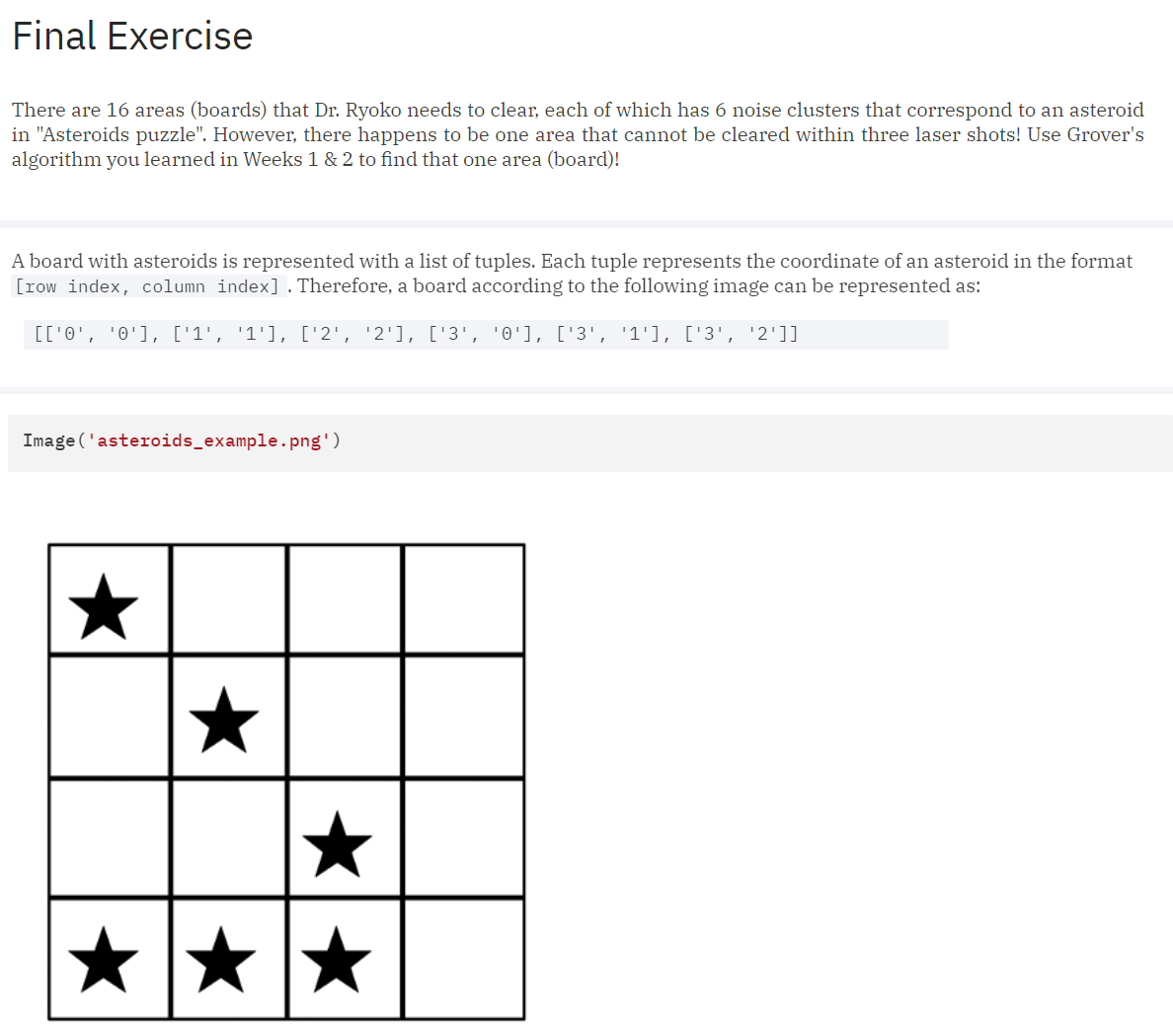
Once the mechanics of the problem understood we are given the full problem statement and a set of rules that must be adhered to for our solutions to be valid. Ultimately the problem boiled down to being given 16 different 4x4 boards where we use Grover's algorithm to determine the single board that is not solvable (clearable) in three laser beam shots.

With the initial background information understood, let's start to solve the problem!

Theoretical Solution

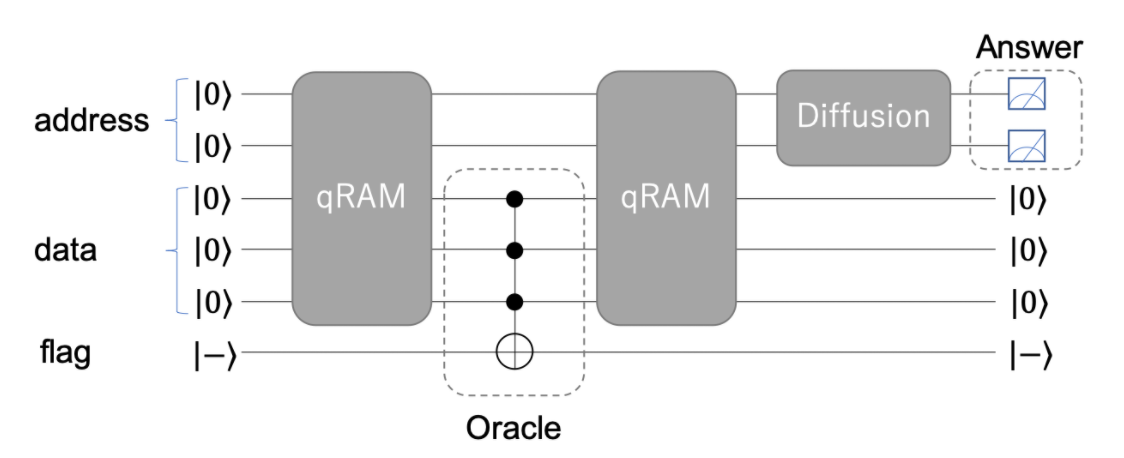
Before writing a single line of code I spent time making sure I conceptually knew how to solve the problem. The first 36 hours of the final week was spent breaking down the various boards and attempting to find clever ways of determining the solution. Starting the overall qRAM structure from the previous week.

The initial thought was to approach the challenge similarly to the second week's lightsout problem - map the boards to the qram addresses, flesh out the 16 qubits representing the board, and codify the mechanics of a laser beam.

There were two inherent problems with this approach. Firstly the limitation on qubits we could leverage was 28. If we were to proceed with this approach we would need 16 for the board representation, 8 for the different laser beam shots (4 vertical, 4 horizontal), 4 for the qram addresses, and finally 1 for the oracle to help amplify winner states. This brings us up to 29 qubits, outside of our limitation. The second limitation in this approach is in the mechanics itself. In the second week's lightsout problem a button push was itself a reversible action. When a button was pushed, any adjoining lights that were on would be turned off and vice-versa. In this final asteroid problem the mechanics were of the nature of "if on, turn off, and stay off", representing destroying the asteroid. Unfortunately trying to leverage something like CNOT gates as we did previously does not work in this context and ultimately the approach would result in a non-reversible mechanic.

After spending some time trying to understand the nature of the problem and what differentiates a solvable and unsolvable board it started making sense when thought of using Linear Algebra. Conceptually a 4x4 board is not solvable in three or less laser beam shots if it has 4 asteroids on distinct rows and columns to each other. Another way of thinking of this is that the 4 asteroids must create a Matrix Rank of 4. Alternatively you can also think of it as these asteroids creating a board having a Determinant not equal to zero, or that it resembles an Identity Matrix. In the context of our problem space as long as there were 4 asteroids that resembled the following, we knew that regardless of the additional two asteroids the board is not solvable in three laser beam shots.

Now that we have a direction we need to figure out how to leverage it. As stated in the rules we are not allowed to preprocess any of the input. We must take the board date and put it into the circuit before any processing is done. This makes it slightly more complicated since we could in theory use classical algorithms to calculate the Determinant. Unfortunately since we do not have the concept of multiplication in Quantum Computing we would need to define our own counters and functions. While not impossible, in fact we worked with adders and counters over the last two weeks, the overall complexity seemed rather high for our problem space. In hindsight since we were essentially working with only 1s and 0s this could have been achieved using a simplified classical function, however I decided to approach it from a different direction.

Two distinct eurka moments led to the first implementation in code. First, we do not "care" where the beams are firing. As long as a board fits a particular configuration we know by the nature of the board itself it is not solvable in three, regardless of where the beams are fired. The second relevation happened while iterating through the various configurations that a 4x4 matrix can have to resemble an Identity Matrix. I quickly realized there were only 24 different combinations, much less that I initially thought there would be. With only 24 permutations this puts us in a good position to leverage Qiskit's Grover Sudoku clause approach where each clause is one of the 24 permutations of a 4x4 Identity Matrix defining that the board has a rank 4 and non-zero determinant. An example clause for the board above would be [0,5,10,15] which also represents the Identity matrix itself. Time to start coding!

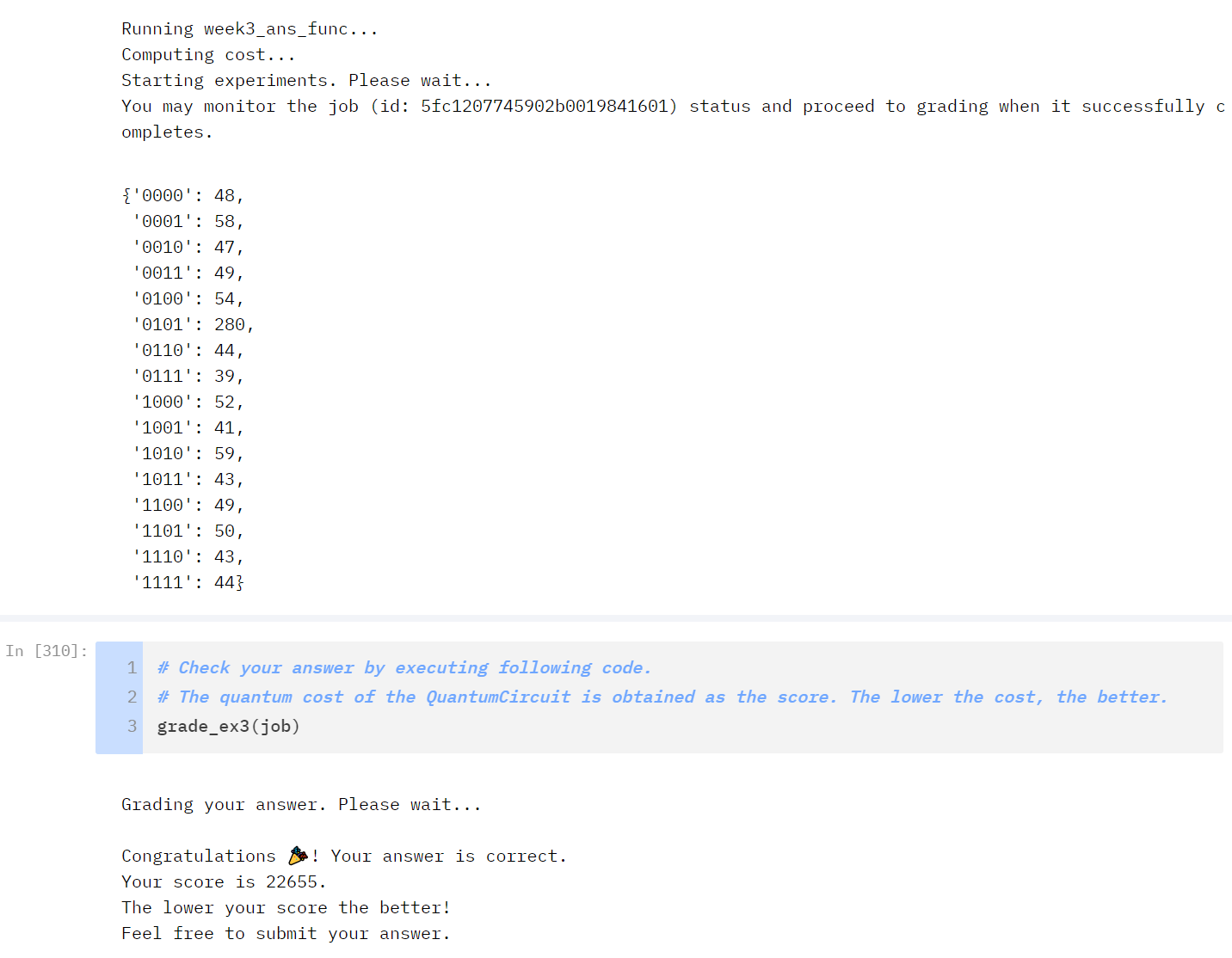
119k - Initial Solution

The theory was essentially broken down into the four parts of the qRAM diagram above.

qRAM the 16 board addresses (0000...1111) in a similar manner we did in the given examples
Run through the various clauses - flipping the oracle if a board matches a configuration
Uncompute the qRAM address
Diffuse the board address, amplifying the non-solvable address

For brevity sake I will try and not include the full code dump and focus on the appropriate snipped sections. My final notebook is available at my Github repo for those interested.

qRAM

We were given the defined problem_set of boards.

problem_set = \
    [[['0', '2'], ['1', '0'], ['1', '2'], ['1', '3'], ['2', '0'], ['3', '3']],
    [['0', '0'], ['0', '1'], ['1', '2'], ['2', '2'], ['3', '0'], ['3', '3']],
    [['0', '0'], ['1', '1'], ['1', '3'], ['2', '0'], ['3', '2'], ['3', '3']],
    [['0', '0'], ['0', '1'], ['1', '1'], ['1', '3'], ['3', '2'], ['3', '3']],
    [['0', '2'], ['1', '0'], ['1', '3'], ['2', '0'], ['3', '2'], ['3', '3']],
    [['1', '1'], ['1', '2'], ['2', '0'], ['2', '1'], ['3', '1'], ['3', '3']],
    [['0', '2'], ['0', '3'], ['1', '2'], ['2', '0'], ['2', '1'], ['3', '3']],
    [['0', '0'], ['0', '3'], ['1', '2'], ['2', '2'], ['2', '3'], ['3', '0']],
    [['0', '3'], ['1', '1'], ['1', '2'], ['2', '0'], ['2', '1'], ['3', '3']],
    [['0', '0'], ['0', '1'], ['1', '3'], ['2', '1'], ['2', '3'], ['3', '0']],
    [['0', '1'], ['0', '3'], ['1', '2'], ['1', '3'], ['2', '0'], ['3', '2']],
    [['0', '0'], ['1', '3'], ['2', '0'], ['2', '1'], ['2', '3'], ['3', '1']],
    [['0', '1'], ['0', '2'], ['1', '0'], ['1', '2'], ['2', '2'], ['2', '3']],
    [['0', '3'], ['1', '0'], ['1', '3'], ['2', '1'], ['2', '2'], ['3', '0']],
    [['0', '2'], ['0', '3'], ['1', '2'], ['2', '3'], ['3', '0'], ['3', '1']],
    [['0', '1'], ['1', '0'], ['1', '2'], ['2', '2'], ['3', '0'], ['3', '1']]]

At which point we can reference and load the appropriate board if the address matches.

def week3_ans_func(problem_set):
    ##### build your quantum circuit here
    ##### In addition, please make it a function that can solve the problem even with different inputs (problem_set). We do validation with different inputs. 
    address = QuantumRegister(4, name='address')
    aux = QuantumRegister(4, name='aux')
    oracle = QuantumRegister(1, name='oracle')
    oracle2 = QuantumRegister(1, name='oracle2')
    tile_qubits = QuantumRegister(16, name='tile')
    address_cbit = ClassicalRegister(4,name='address-c')
    #classical2 = ClassicalRegister(16,name='tile-c')
    qc = QuantumCircuit(address,tile_qubits,aux,oracle,oracle2,address_cbit)

    ##init qubits
    qc.h(address)
    
    #############################
    ##### QRAM Init
    #############################
    # address 0 - 0000
    qc.x([address[0],address[1],address[2],address[3]])
    for asteroid in problem_set[0]:
                num = int(asteroid[0]) * 4
                num += int(asteroid[1])
                qc.mct(address,tile_qubits[num])
    qc.x([address[0],address[1],address[2],address[3]])
    # address 1 - 0001
    qc.x([address[0],address[1],address[2]])
    for asteroid in problem_set[1]:
                num = int(asteroid[0]) * 4
                num += int(asteroid[1])
                qc.mct(address,tile_qubits[num])
    qc.x([address[0],address[1],address[2]])
    # address 2 - 0010
    qc.x([address[0],address[1],address[3]])
    for asteroid in problem_set[2]:
                num = int(asteroid[0]) * 4
                num += int(asteroid[1])
                qc.mct(address,tile_qubits[num])
    qc.x([address[0],address[1],address[3]])
    # address 3 - 0011
    qc.x([address[0],address[1]])
    for asteroid in problem_set[3]:
                num = int(asteroid[0]) * 4
                num += int(asteroid[1])
                qc.mct(address,tile_qubits[num])
    qc.x([address[0],address[1]])
    # address 4 - 0100
... <snip>...

Continuing down for all 16 addresses. This qRAM section is also used for the qRAM uncompute portion of the flow.

Grover Oracle

Once we had the board loaded we iterate through the 24 clauses and flip the oracle if set.

    for i in range(1):
    
        ################################
        ##### START of - Grover
        ################################
        
        ## Iterate through clause list of potentials - Crude version for determining rank4 matrix
        
        ################ 0's
        #0,5,10,15
        qc.mct([tile_qubits[0],tile_qubits[5],tile_qubits[10],tile_qubits[15]],aux[0]) 
        qc.cx(aux[0],oracle)
        qc.ccx(aux[0],oracle,oracle2)
        qc.mct([tile_qubits[0],tile_qubits[5],tile_qubits[10],tile_qubits[15]],aux[0]) 
        #0,5,11,14
        qc.mct([tile_qubits[0],tile_qubits[5],tile_qubits[11],tile_qubits[14]],aux[0])
        qc.cx(aux[0],oracle)
        qc.ccx(aux[0],oracle,oracle2)
        qc.mct([tile_qubits[0],tile_qubits[5],tile_qubits[11],tile_qubits[14]],aux[0])
        #0,6,9,15
        qc.mct([tile_qubits[0],tile_qubits[6],tile_qubits[9],tile_qubits[15]],aux[0])
        qc.cx(aux[0],oracle)
        qc.ccx(aux[0],oracle,oracle2)
        qc.mct([tile_qubits[0],tile_qubits[6],tile_qubits[9],tile_qubits[15]],aux[0])
        #0,6,11,13
        qc.mct([tile_qubits[0],tile_qubits[6],tile_qubits[11],tile_qubits[13]],aux[0])
        qc.cx(aux[0],oracle)
        qc.ccx(aux[0],oracle,oracle2)
        qc.mct([tile_qubits[0],tile_qubits[6],tile_qubits[11],tile_qubits[13]],aux[0])
        ...<snip>...

Of note here is the double oracles. Since a clause is 4 asteroids and there are 6 asteroids on the board we need to take into consideration a board where two clauses are satisfied by the 6 asteroids. Example below where the board satisfies both [0,5,10,15] as well as [1,4,10,15].

If we were to just flip the oracle when a clause is met, any board that satisfies two clauses would ultimately turn off the oracle. Since we know that at most two clauses can be satisfied by a single, 6-asteroid board, we only need to consider a double oracle situation, and not >2 potential clause satisfying boards.

Diffusion

Standard qRAM address diffusion we leveraged in the previous week's examples.

    qc.h(address)
    qc.x(address)
    qc.h(address[-1])
    qc.mct(address[:-1], address[-1])
    qc.h(address[-1])
    qc.x(address)
    qc.h(address)

Submission

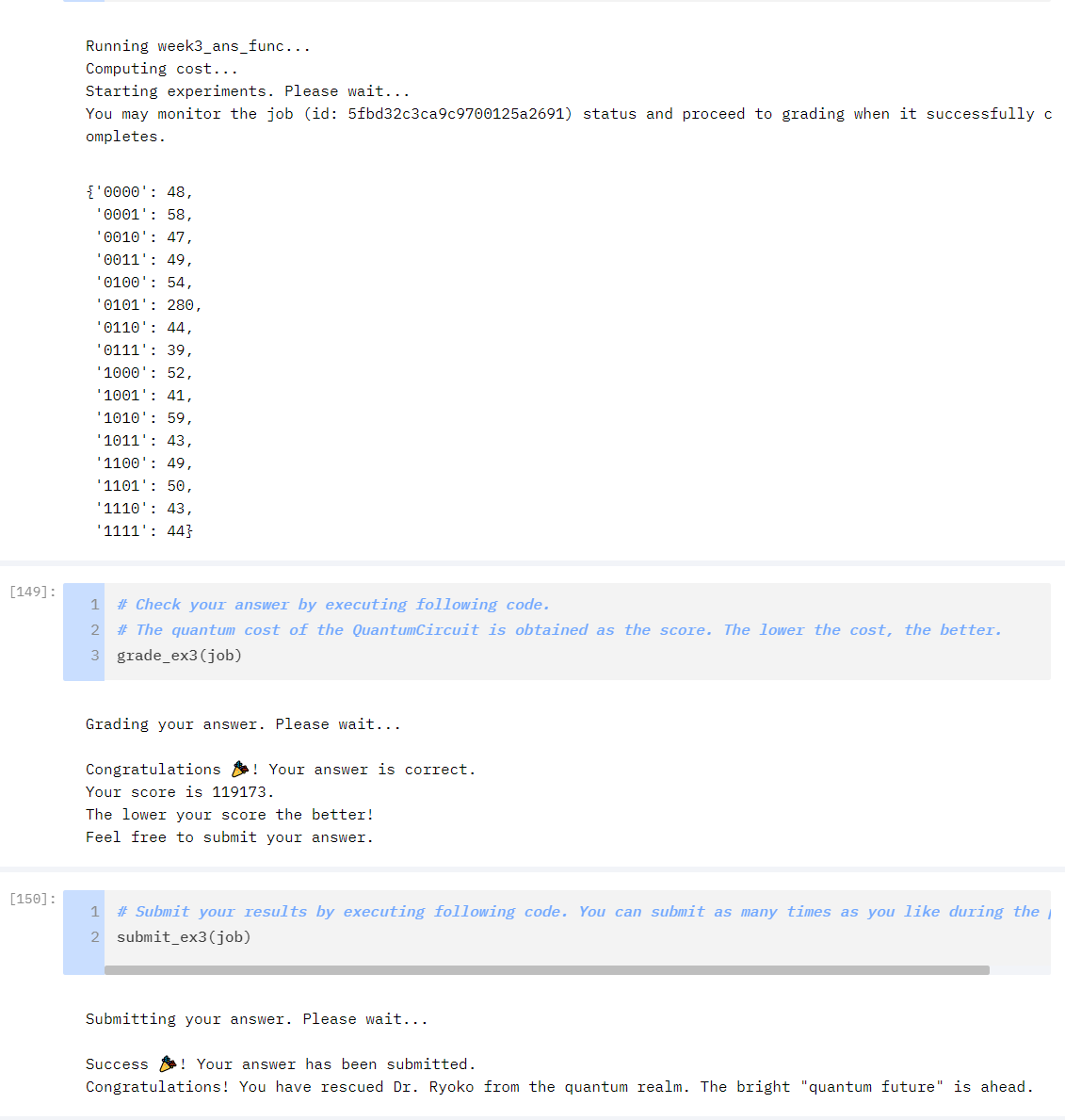
With the code setup I submitted the job and put on another pot of coffee while it processed. After about ~20 minutes I was happy to report that it successfully worked!

This is just the start however, as now the improvement iterations can start!

53k - Ancillary Qubits

The first improvement iteration was conceptually simple. Originally we executed straight MCTs on the address/oracle portions. Let's add some ancillary qubits help bring that cost down since we have a few to work with within the 28 qubit limitation.

    # address 0 - 0000
    qc.x([address[0],address[1],address[2],address[3]])
    for asteroid in problem_set[0]:
                num = int(asteroid[0]) * 4
                num += int(asteroid[1])
                qc.mct(address,tile_qubits[num], anc, mode="basic")
    qc.x([address[0],address[1],address[2],address[3]])

        ## Iterate through clause list of potentials - Crude version for determining rank4 matrix
        ################ 0's
        #0,5,10,15
        qc.mct([tile_qubits[0],tile_qubits[5],tile_qubits[10],tile_qubits[15]],aux[0], anc, mode="basic") 
        qc.cx(aux[0],oracle)
        qc.ccx(aux[0],oracle,oracle2)
        qc.mct([tile_qubits[0],tile_qubits[5],tile_qubits[10],tile_qubits[15]],aux[0], anc, mode="basic")

At this point I also want to introduce a nifty little code snippet. With a second notebook open I was able to leverage the below to do cost evaluations of the circuit without executing the full ~20 min runs. This helped immensely when I wasn't sure if the approach was worth persuing or not.

from qiskit.transpiler.passes import Unroller
from qiskit.transpiler import PassManager

pass_ = Unroller(['u3', 'cx'])
pm = PassManager(pass_)
new_circuit = pm.run(qc) 
odict = new_circuit.count_ops()
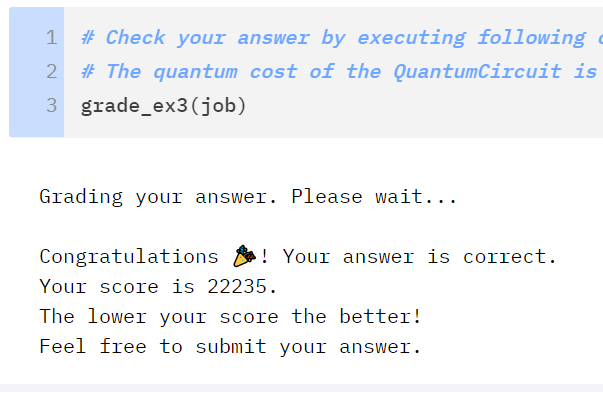
print('u3:'+str(odict['u3'])+' ''cx:'+str(odict['cx'])+' '+'total:'+str(odict['u3']+10*odict['cx']))

With this we can throw portions of circuit into this notebook an breakdown the cost of each. With our introduced ancillary qubits we get to a total complexity cost of 53k. Already less than half of the original solution.

u3:8307 cx:4502 total:53327
Qram - 20512
Oracle - 12144
Qram - 20512
Diffuse - 159

22k - MCMT/Gray Code

This particular iteration is my favourite mostly of how it came to me. During the middle of the week I was going over the qRAM and oracle portions trying to identify where I could simplify the execution. During a morning shower I came to a sudden realization that for the qRAM portions I am running an MCT gate for EACH of the six asteroids. If we know the address is valid, we should be able to find a way cut down to a simpler comparison. I quickly mocked up the pseudocode on the shower door and made sure my logic made sense. I was then able to implement the code improvement later in the day.

    # address 0 - 0000
    qc.x([address[0],address[1],address[2],address[3]])
    qc.mct(address,aux[0], anc, mode="basic")
    for asteroid in problem_set[0]:
                num = int(asteroid[0]) * 4
                num += int(asteroid[1])
                qc.cx(aux[0],tile_qubits[num])
    qc.mct(address,aux[0], anc, mode="basic")          
    # address 1 - 0001
    qc.x(address[3])
    qc.mct(address,aux[0], anc, mode="basic")
    for asteroid in problem_set[1]:
                num = int(asteroid[0]) * 4
                num += int(asteroid[1])
                qc.cx(aux[0],tile_qubits[num])
    qc.mct(address,aux[0], anc, mode="basic")

By pulling out MCT gates from within the loop and using an additional aux qubit to determine when the address is triggered we can replace 6 MCT gates with 2 MCT and 6 CX gates.

The observant reader will also notice I changed the qRAM address method as well. Instead of running X gates before and after to reset we are able to leverage Gray Code ordering to reduce a very small amount of gates for the qRAM address iteration.

Sadly, despite the eureka shower moment and finding a manual approach to reducing I soon found the MCMT (Multi-Control Multi-Target) gate. Using MCMTs ever so slightly increased efficiency, by a total of 12 cost per qRAM address, depite resulting in much uglier code.

    # address 0 - 0000
    qc.x([address[0],address[1],address[2],address[3]])    
    qc.mcmt(qc.cx,address,[tile_qubits[int(problem_set[0][0][0])*4+int(problem_set[0][0][1])],tile_qubits[int(problem_set[0][1][0])*4+int(problem_set[0][1][1])],tile_qubits[int(problem_set[0][2][0])*4+int(problem_set[0][2][1])],tile_qubits[int(problem_set[0][3][0])*4+int(problem_set[0][3][1])],tile_qubits[int(problem_set[0][4][0])*4+int(problem_set[0][4][1])],tile_qubits[int(problem_set[0][5][0])*4+int(problem_set[0][5][1])]],anc,mode='basic')
    # address 1 - 0001
    qc.x(address[3])
    qc.mcmt(qc.cx,address,[tile_qubits[int(problem_set[1][0][0])*4+int(problem_set[1][0][1])],tile_qubits[int(problem_set[1][1][0])*4+int(problem_set[1][1][1])],tile_qubits[int(problem_set[1][2][0])*4+int(problem_set[1][2][1])],tile_qubits[int(problem_set[1][3][0])*4+int(problem_set[1][3][1])],tile_qubits[int(problem_set[1][4][0])*4+int(problem_set[1][4][1])],tile_qubits[int(problem_set[1][5][0])*4+int(problem_set[1][5][1])]],anc,mode='basic')

At the end of this iteration I was able to further reduce the complexity cost from 192 MCT gates, to 64 MCT + 192 CX, to 32 MCMT gates, and ultimately got the cost down to 22k.

51k - MCT Decomposition

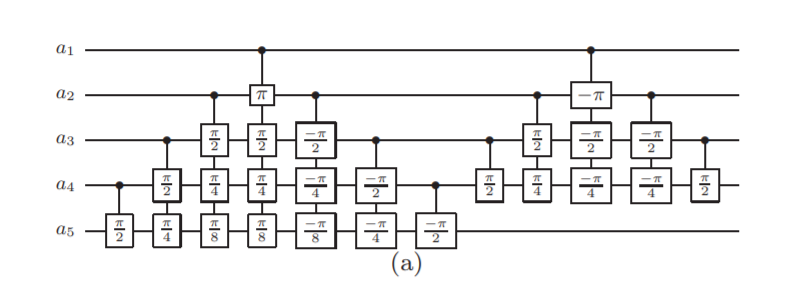
This iteration made the writeup not because it was more efficient. In fact it was worst than all but the original solution. It made this writeup however because of how it was implemented. While searching through various papers for academically inspired decompositions I ran into Linear-Depth Quantum Circuits for n-qubit Toffoli gates with no Ancilla. The interesting aspect of this paper was that it decomposed an MCT gate without ancillary qubits achieving a linear speed up to regular MCT gates. The approached was summarized in the following graph.

Feeling inspired I strived to implement it in my circuit and see how it fared in complexity cost.

qc.x([address[0],address[1],address[2],address[3]])
for asteroid in problem_set[0]:
num = int(asteroid[0]) * 4
num += int(asteroid[1])
#qc.mct(address,tile_qubits[num], anc, mode="basic")
qc.rxx(math.pi/2,address[0],address[1])
qc.rxx(math.pi/4,address[0],address[2])
qc.rxx(math.pi/8,address[0],address[3])
qc.rxx(math.pi/8,address[0],tile_qubits[num])
qc.rxx(math.pi/2,address[1],address[2])
qc.rxx(math.pi/4,address[1],address[3])
qc.rxx(math.pi/4,address[1],tile_qubits[num])
qc.rxx(math.pi/2,address[2],address[3])
qc.rxx(math.pi/2,address[2],tile_qubits[num])
qc.rxx(math.pi,address[3],tile_qubits[num])
qc.rxx(-math.pi/2,address[2],address[3])
qc.rxx(-math.pi/4,address[1],address[3])
qc.rxx(-math.pi/2,address[1],address[2])
qc.rxx(-math.pi/8,address[0],address[3])
qc.rxx(-math.pi/4,address[0],address[2])
qc.rxx(-math.pi/2,address[0],address[1])

qc.rxx(math.pi/2,address[1],address[2])
qc.rxx(math.pi/4,address[1],address[3])
qc.rxx(-math.pi/4,address[1],tile_qubits[num])
qc.rxx(math.pi/2,address[2],address[3])
qc.rxx(-math.pi/2,address[2],tile_qubits[num])
qc.rxx(-math.pi,address[3],tile_qubits[num])
qc.rxx(-math.pi/2,address[2],address[3])
qc.rxx(-math.pi/4,address[1],address[3])
qc.rxx(math.pi/2,address[1],address[2])

I was able to get a result, however it was clearly not as efficient as what we had already achieved. Interesting nonetheless as it was the first time I used a pure academic paper and tried to implement it.

20k - RCCX Oracle

This next iteration leveraged the hints that the Qiskit team provided in week two - gate synthesis or equivalence transformation techniques. Specifically leveraging the RCCX gate example.

Since we were performing uncomputes throughout the circuit we should be able to break down MCT gates to their CCX/CX equivalents and then replace CCX with RCCX gates to save on cost. One additional improvement I realized at this point was related to the clause combination. Since the first two qubits of each clause pair ([0,5,10,15] and [0,5,11,14] as examples) are the same, we should be able to reduce the amount of overall comparisons done if we change only the 3rd and 4th qubits between pairs.

#0,5,10,15
#0,5,11,14
qc.rccx(tile_qubits[0],tile_qubits[5],aux[0])
qc.rccx(tile_qubits[10],tile_qubits[15],aux[1])
qc.swap(oracle,oracle2)
qc.rccx(aux[0],aux[1],oracle) #checking for 0,5,10,15
qc.swap(oracle,oracle2)
qc.rccx(tile_qubits[10],tile_qubits[15],aux[1])
qc.rccx(tile_qubits[11],tile_qubits[14],aux[1])
qc.swap(oracle,oracle2)
qc.rccx(aux[0],aux[1],oracle) #checking for 0,5,11,14
qc.swap(oracle,oracle2)
qc.rccx(tile_qubits[11],tile_qubits[14],aux[1])
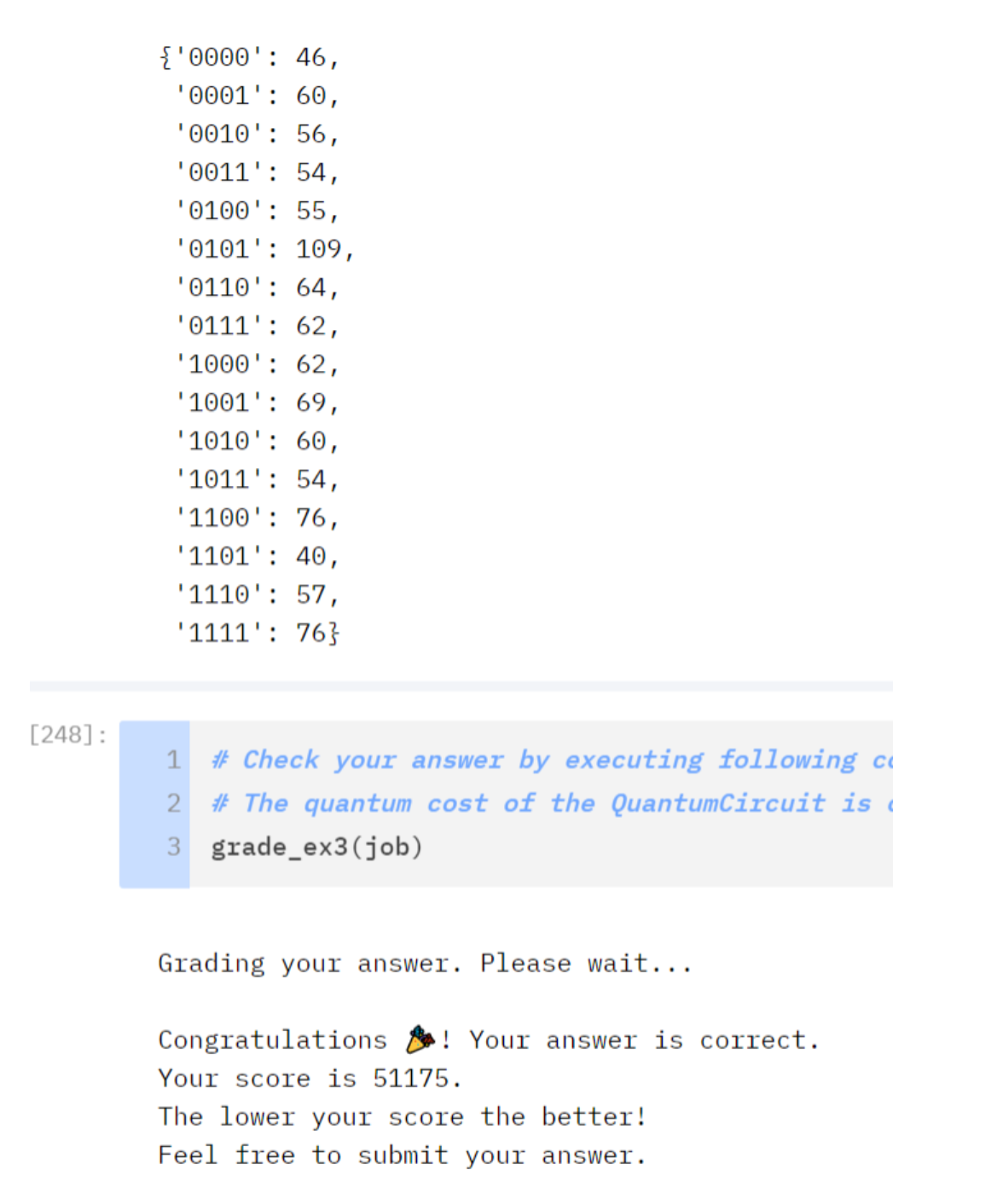
qc.rccx(tile_qubits[0],tile_qubits[5],aux[0])

QRAM - u3:886 cx:672 total:7606
Oracle - u3:576 cx:432 total:4896
QRAM - u3:890 cx:672 total:7606
Diffuse - u3:39 cx:12 total:159

13k - RCCX qRAM

This particular iteration was taking the same methodology from the 20k variant and applying RCCX gates to the qRAM portions. I had to go back from the MCMT variants to MCT gates and break down the MCT to CCX/CX as above before transforming to RCCX gates.

qc.x([address[0],address[1],address[2],address[3]])
#qc.mcmt(qc.cx,address,[tile_qubits[int(problem_set[0][0][0])*4+int(problem_set[0][0][1])],tile_qubits[int(problem_set[0][1][0])*4+int(problem_set[0][1][1])],tile_qubits[int(problem_set[0][2][0])*4+int(problem_set[0][2][1])],tile_qubits[int(problem_set[0][3][0])*4+int(problem_set[0][3][1])],tile_qubits[int(problem_set[0][4][0])*4+int(problem_set[0][4][1])],tile_qubits[int(problem_set[0][5][0])*4+int(problem_set[0][5][1])]],aux,mode='basic')
qc.rccx(address[0],address[1],aux[0])
qc.rccx(address[2],address[3],aux[1])
qc.rccx(aux[0],aux[1],aux[3])
qc.cx(aux[3],tile_qubits[int(problem_set[0][0][0])*4+int(problem_set[0][0][1])])
qc.cx(aux[3],tile_qubits[int(problem_set[0][1][0])*4+int(problem_set[0][1][1])])
qc.cx(aux[3],tile_qubits[int(problem_set[0][2][0])*4+int(problem_set[0][2][1])])
qc.cx(aux[3],tile_qubits[int(problem_set[0][3][0])*4+int(problem_set[0][3][1])])
qc.cx(aux[3],tile_qubits[int(problem_set[0][4][0])*4+int(problem_set[0][4][1])])
qc.cx(aux[3],tile_qubits[int(problem_set[0][5][0])*4+int(problem_set[0][5][1])])
qc.rccx(aux[0],aux[1],aux[3])
qc.rccx(address[2],address[3],aux[1])
qc.rccx(address[0],address[1],aux[0])
# address 1 - 0001
qc.x(address[3])
#qc.mcmt(qc.cx,address,[tile_qubits[int(problem_set[1][0][0])*4+int(problem_set[1][0][1])],tile_qubits[int(problem_set[1][1][0])*4+int(problem_set[1][1][1])],tile_qubits[int(problem_set[1][2][0])*4+int(problem_set[1][2][1])],tile_qubits[int(problem_set[1][3][0])*4+int(problem_set[1][3][1])],tile_qubits[int(problem_set[1][4][0])*4+int(problem_set[1][4][1])],tile_qubits[int(problem_set[1][5][0])*4+int(problem_set[1][5][1])]],aux,mode='basic')
qc.rccx(address[0],address[1],aux[0])
qc.rccx(address[2],address[3],aux[1])
qc.rccx(aux[0],aux[1],aux[3])
qc.cx(aux[3],tile_qubits[int(problem_set[1][0][0])*4+int(problem_set[1][0][1])])
qc.cx(aux[3],tile_qubits[int(problem_set[1][1][0])*4+int(problem_set[1][1][1])])
qc.cx(aux[3],tile_qubits[int(problem_set[1][2][0])*4+int(problem_set[1][2][1])])
qc.cx(aux[3],tile_qubits[int(problem_set[1][3][0])*4+int(problem_set[1][3][1])])
qc.cx(aux[3],tile_qubits[int(problem_set[1][4][0])*4+int(problem_set[1][4][1])])
qc.cx(aux[3],tile_qubits[int(problem_set[1][5][0])*4+int(problem_set[1][5][1])])
qc.rccx(aux[0],aux[1],aux[3])
qc.rccx(address[2],address[3],aux[1])
qc.rccx(address[0],address[1],aux[0])

QRAM - u3:598 cx:384 total:4438
Oracle - u3:576 cx:432 total:4896
QRAM - u3:598 cx:384 total:4438
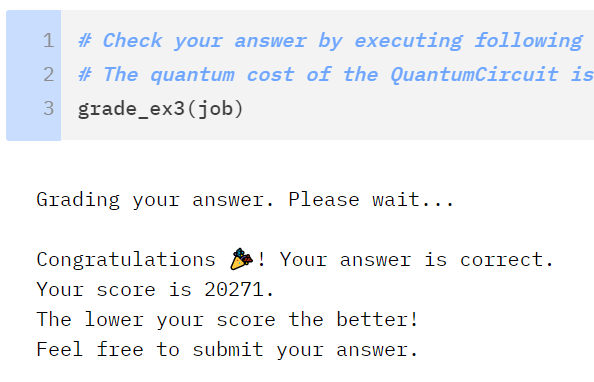
Diffuse - u3:39 cx:12 total:159

With what seemed like the regular statement throughout this entire process I told myself I did not believe the cost could be lowered further without fundamentally changing the structure of my approach. There were other solutions submitted in the 7k range at this point and I was almost certain they were approaching the problem differently. Based on the RCCX/CCX/CX decompositions I thought I had done as much as I could. I was wrong...

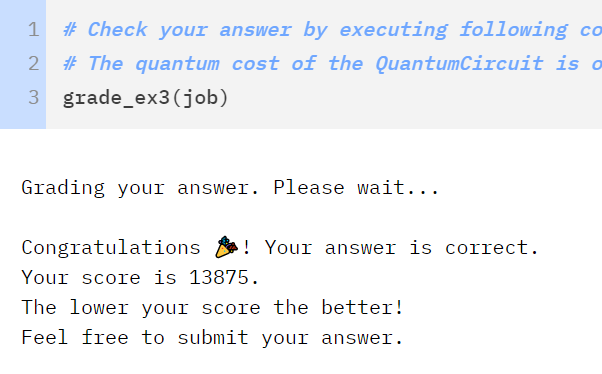
12k - Here Be Dragons

Everything I went through prior to this section can be thought of with classical circuits and makes logical sense more or less as you step through the code in 2 dimensional terms. This last iteration jumps off the deep end by leveraging quantum phases. I can honestly say that the jump from 13k to 12k is where I learned the most out of this entire journey.

As was mentioned above in the original rules of the challenge our solution could not include any runs of transpiler to simplify the circuit design. Out of interest I took my 13k circuit above and ran it through transpiler on a second notebook to see if the cost would go down. Sure enough it resulted in sub-10k complexity costs so I knew there was still work to do.

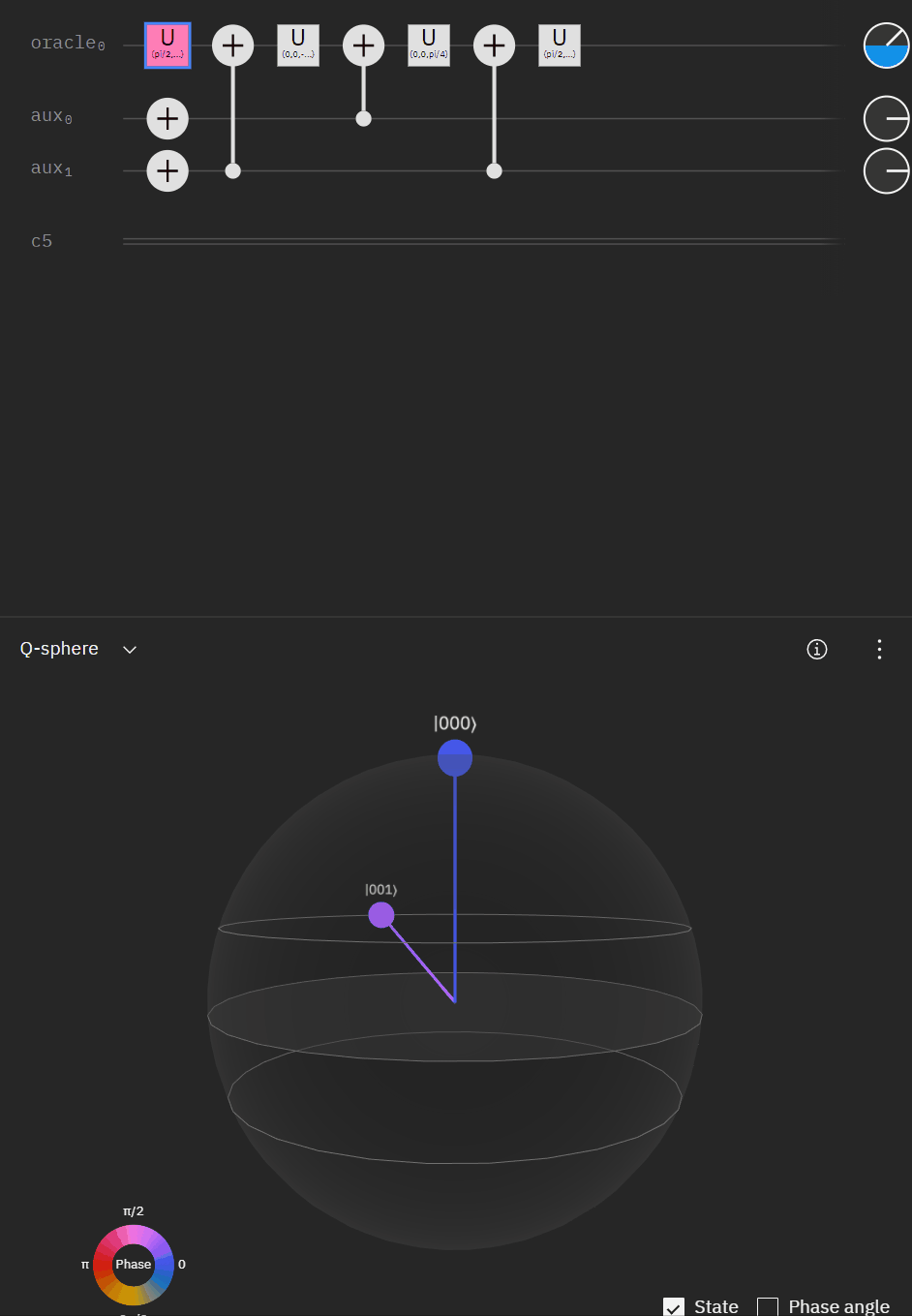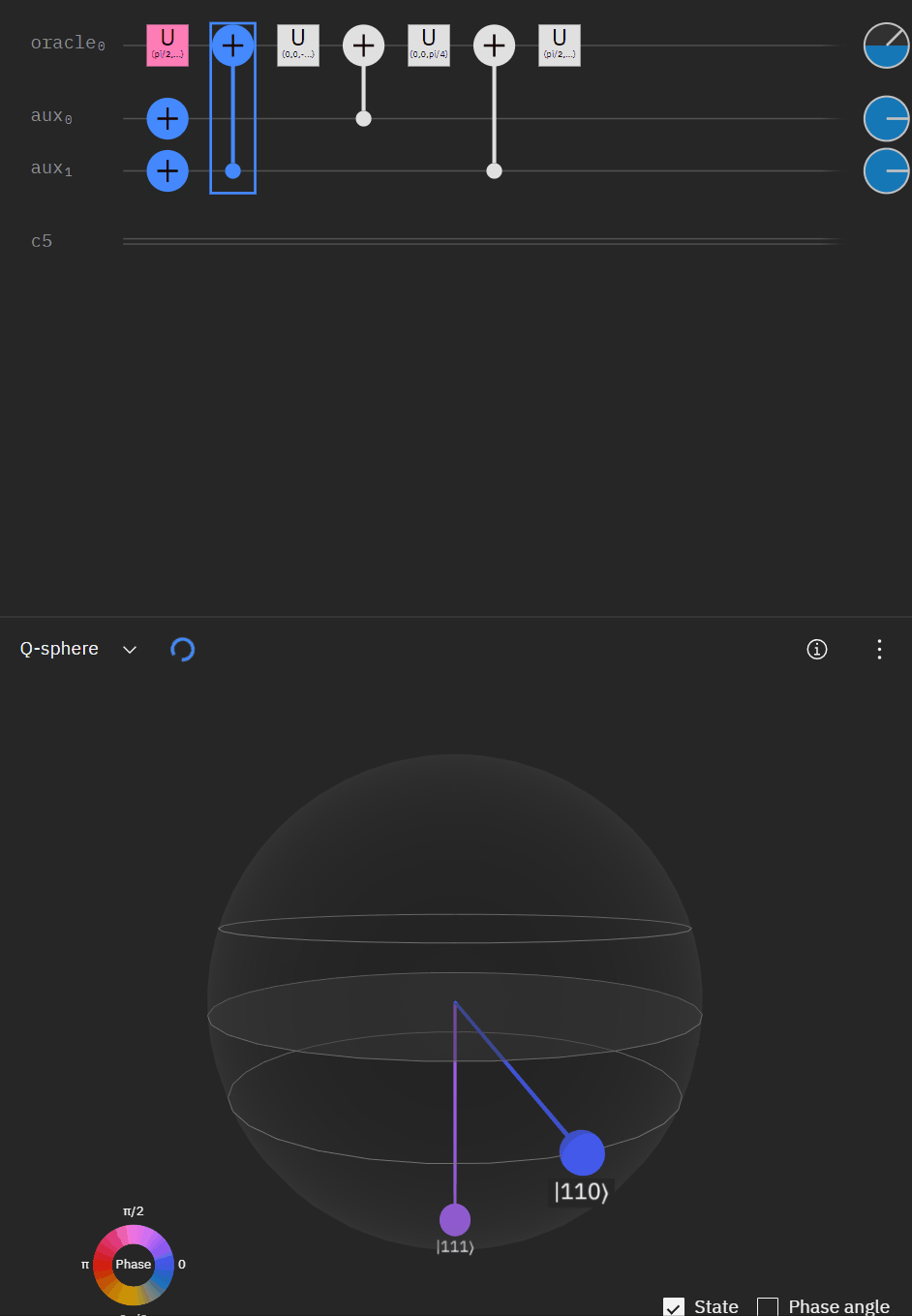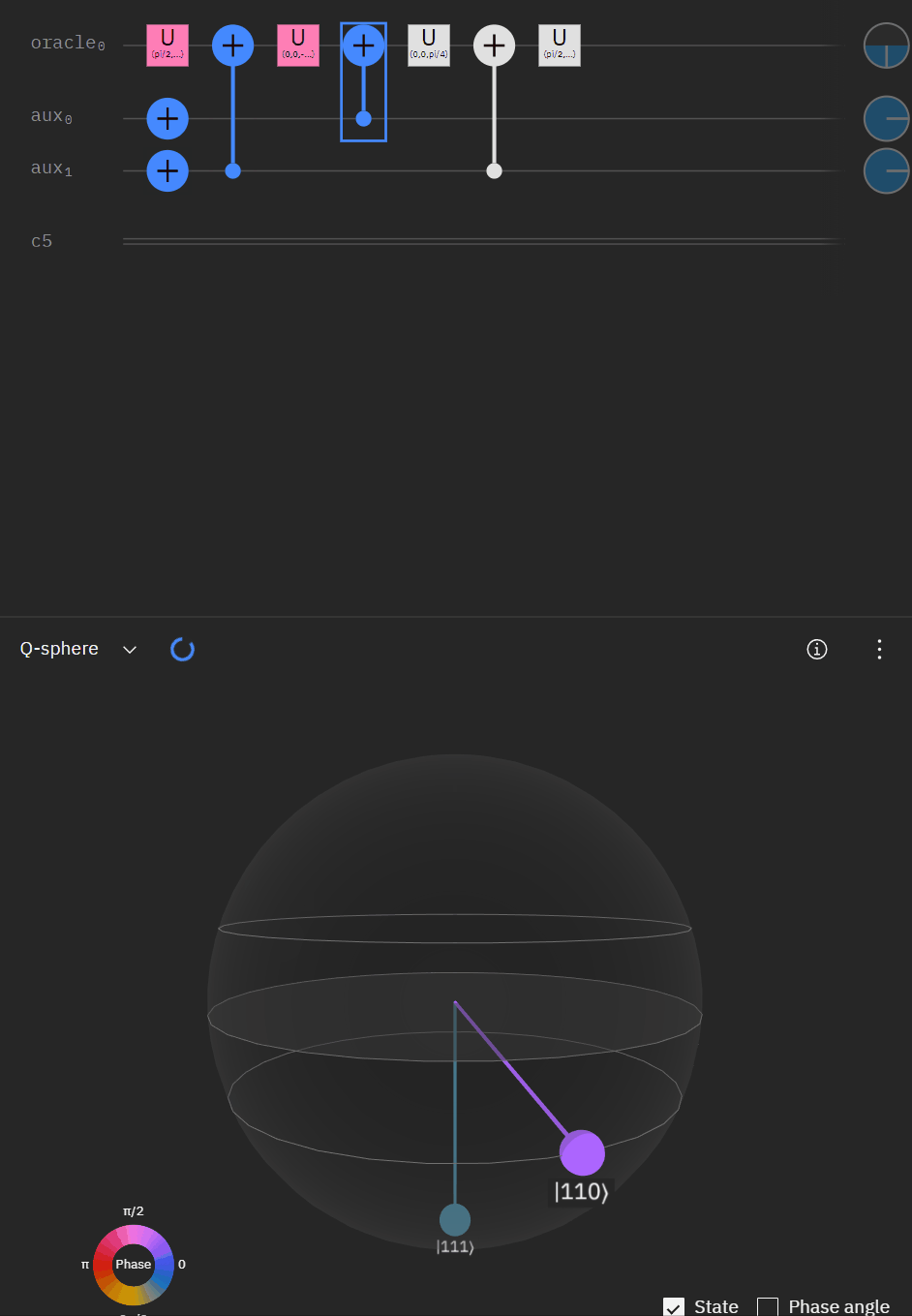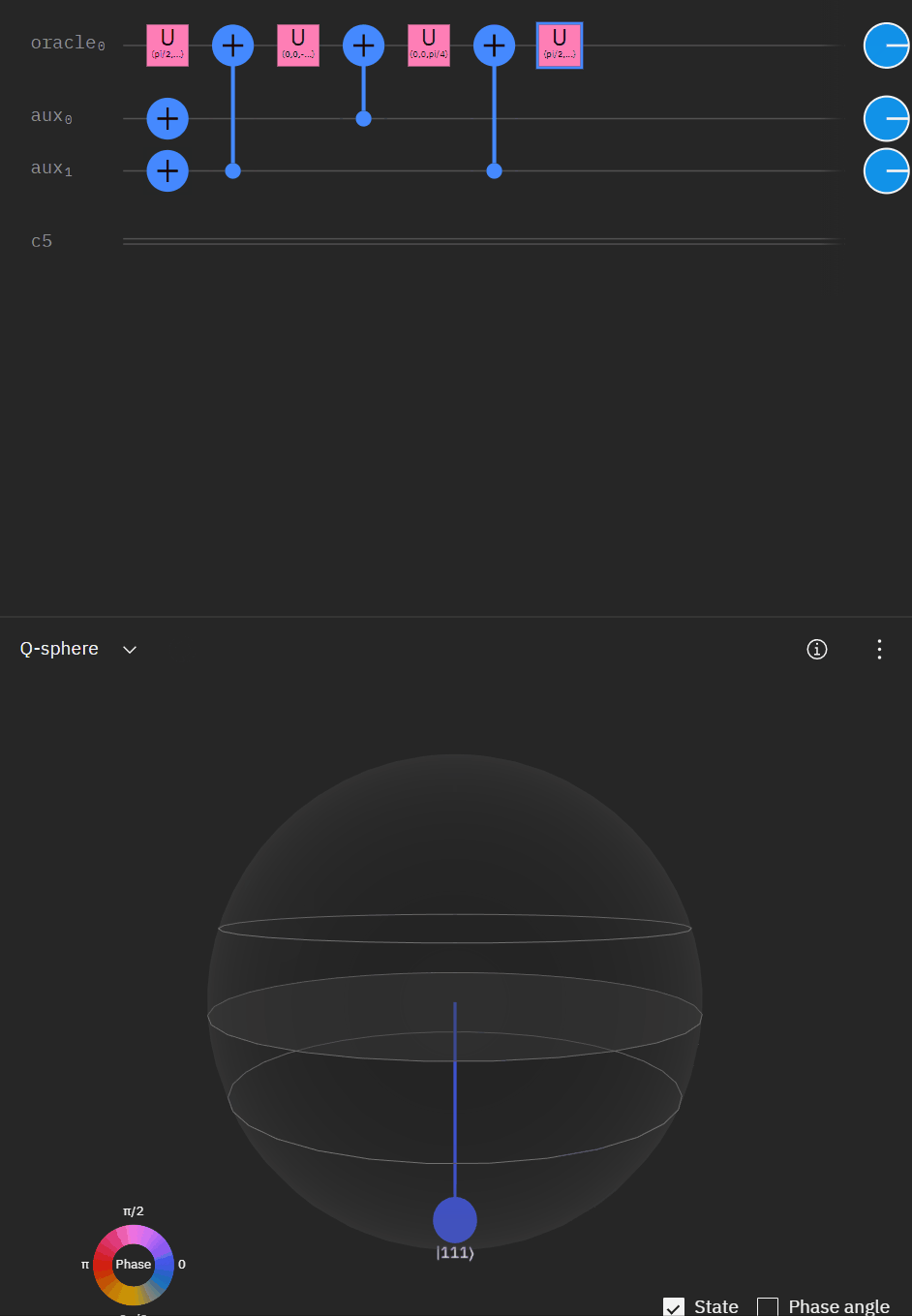
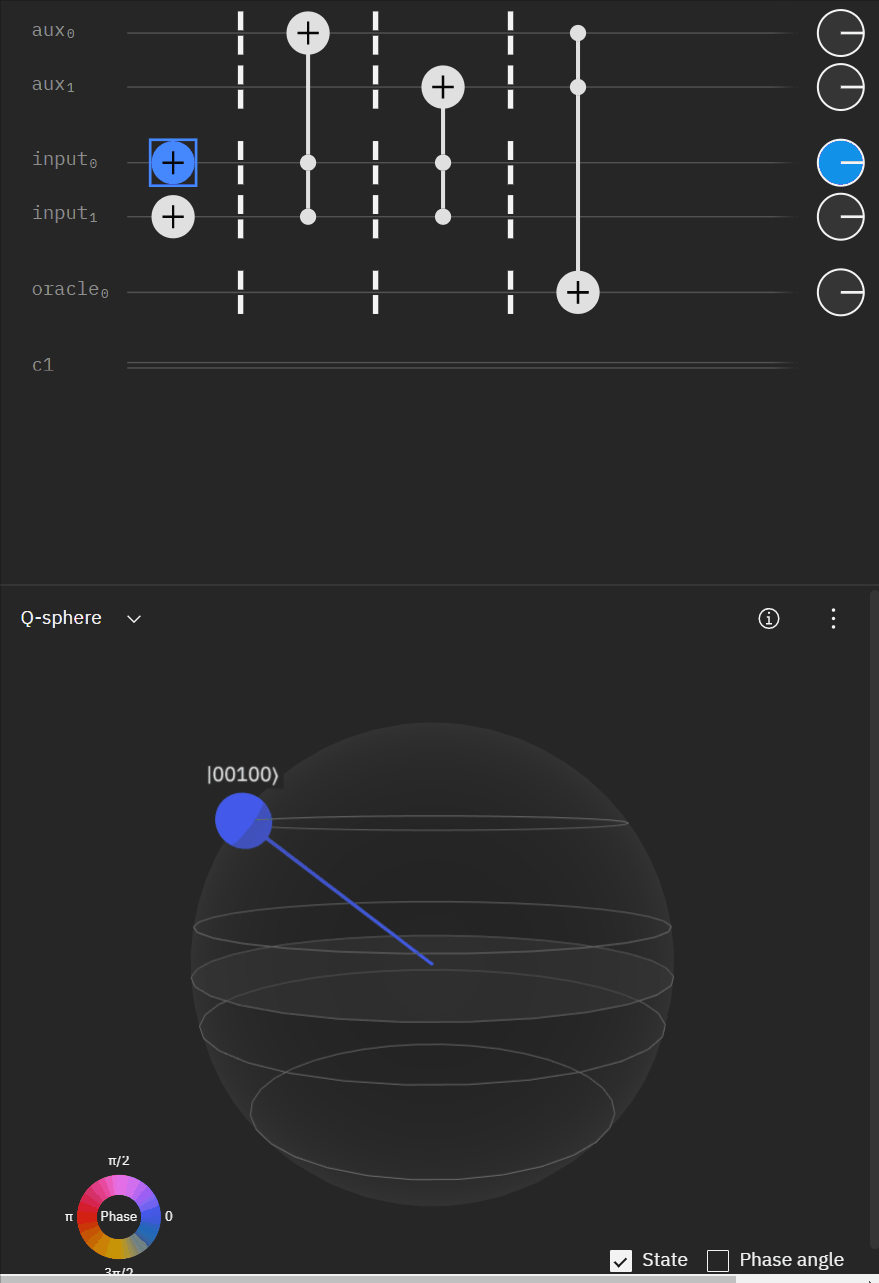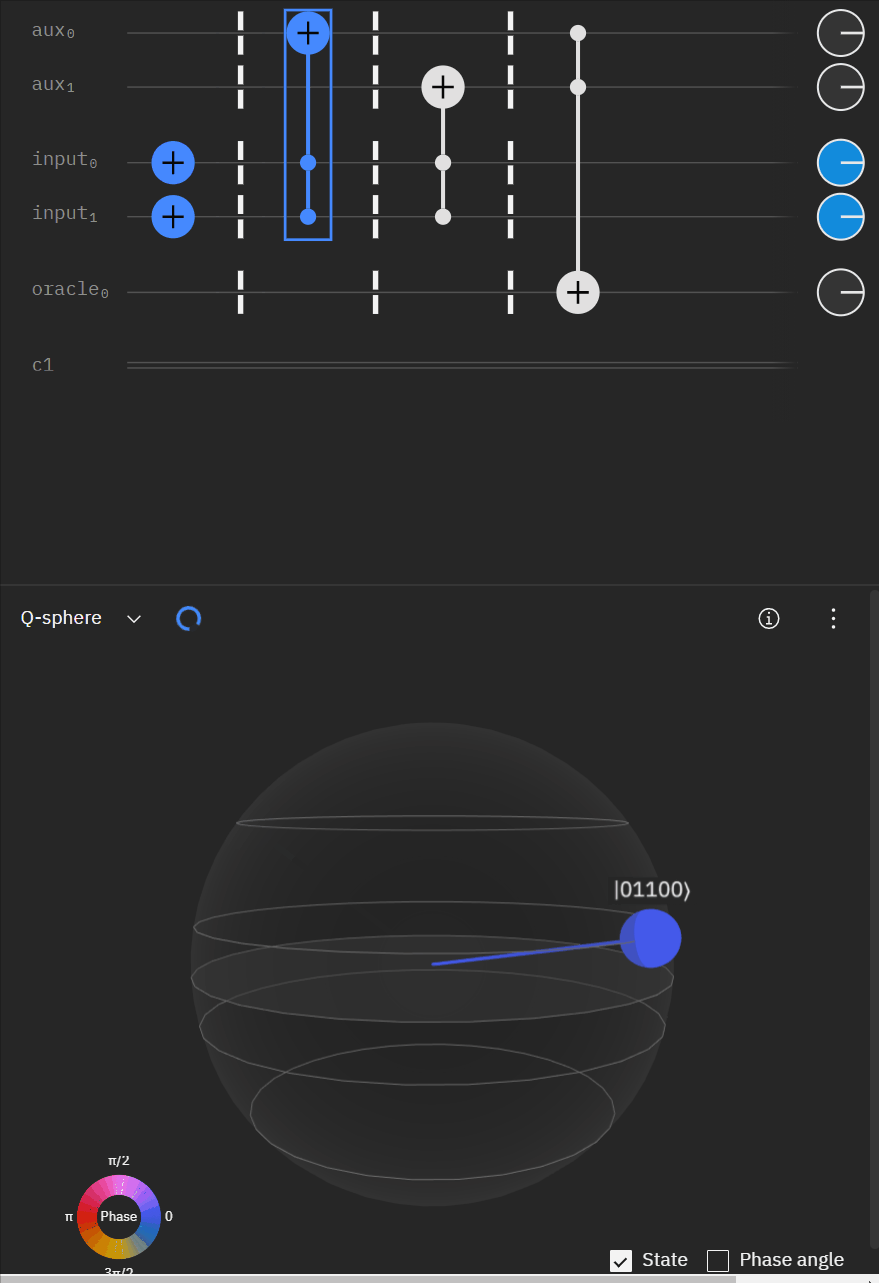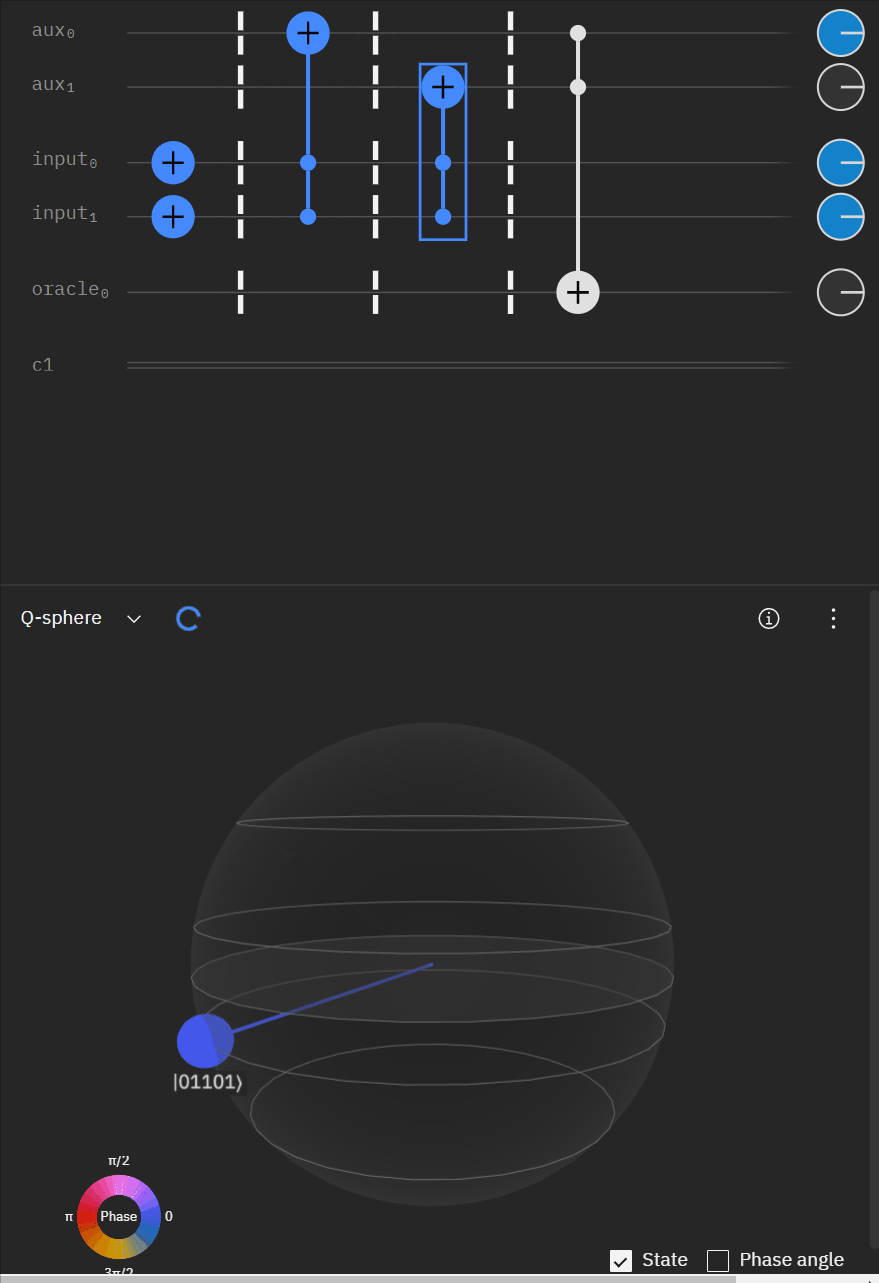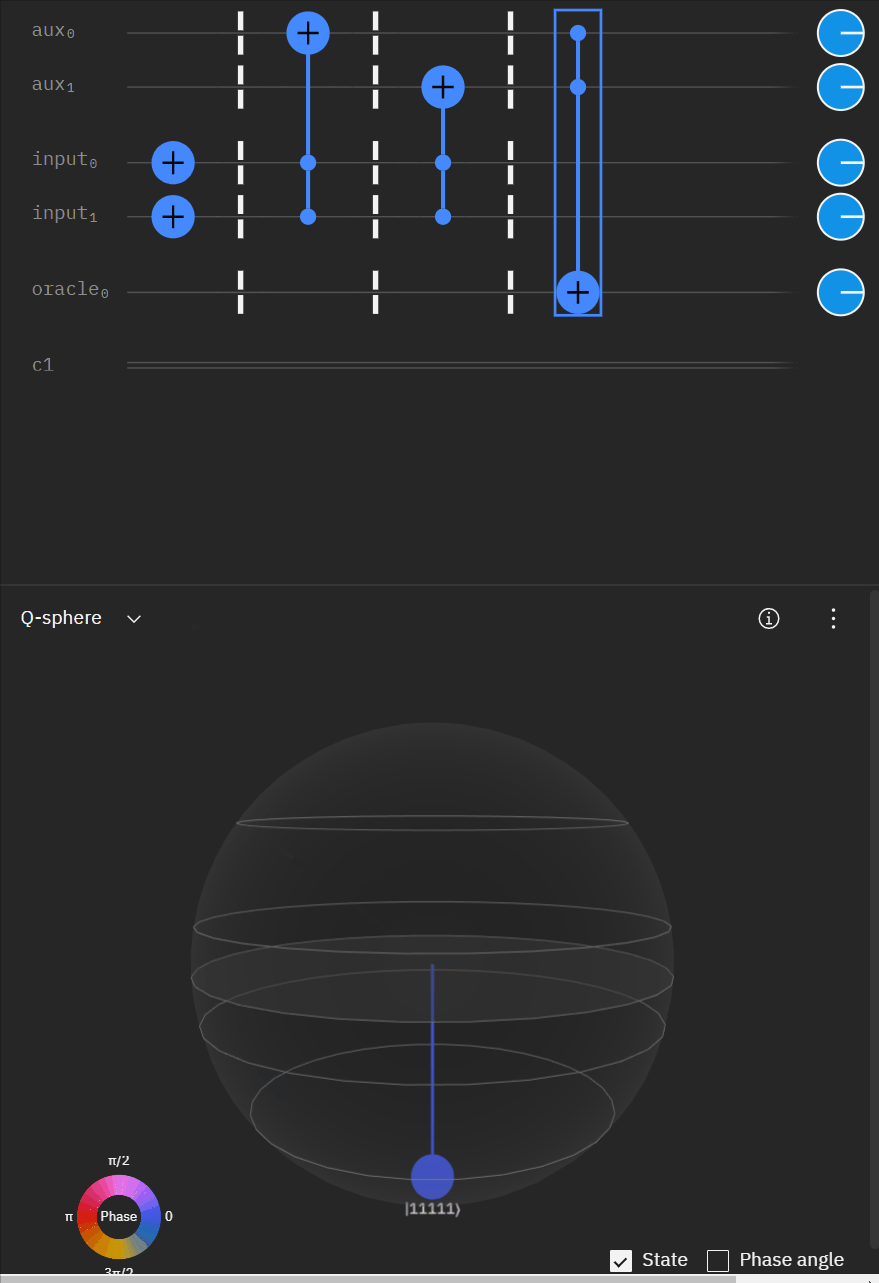
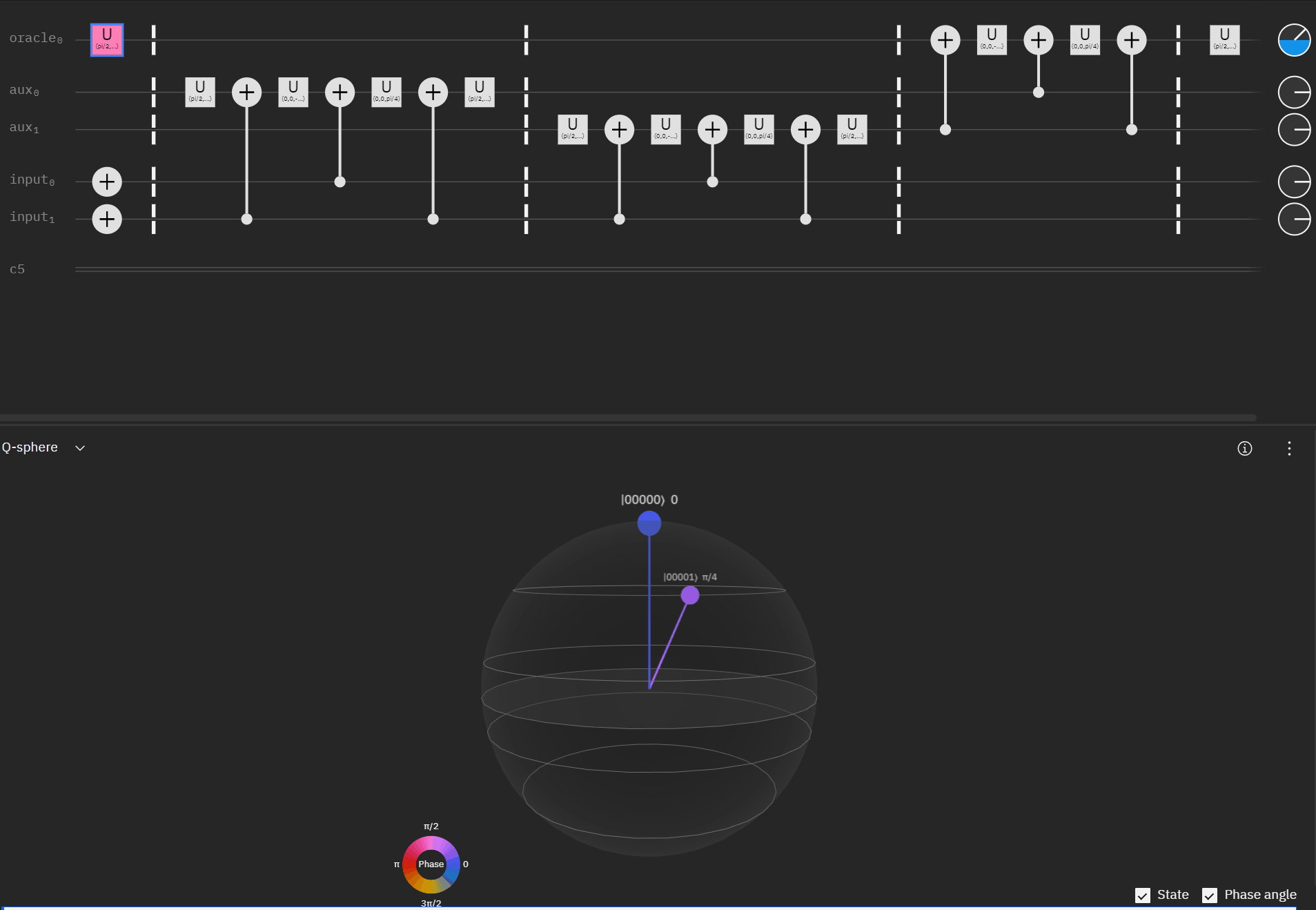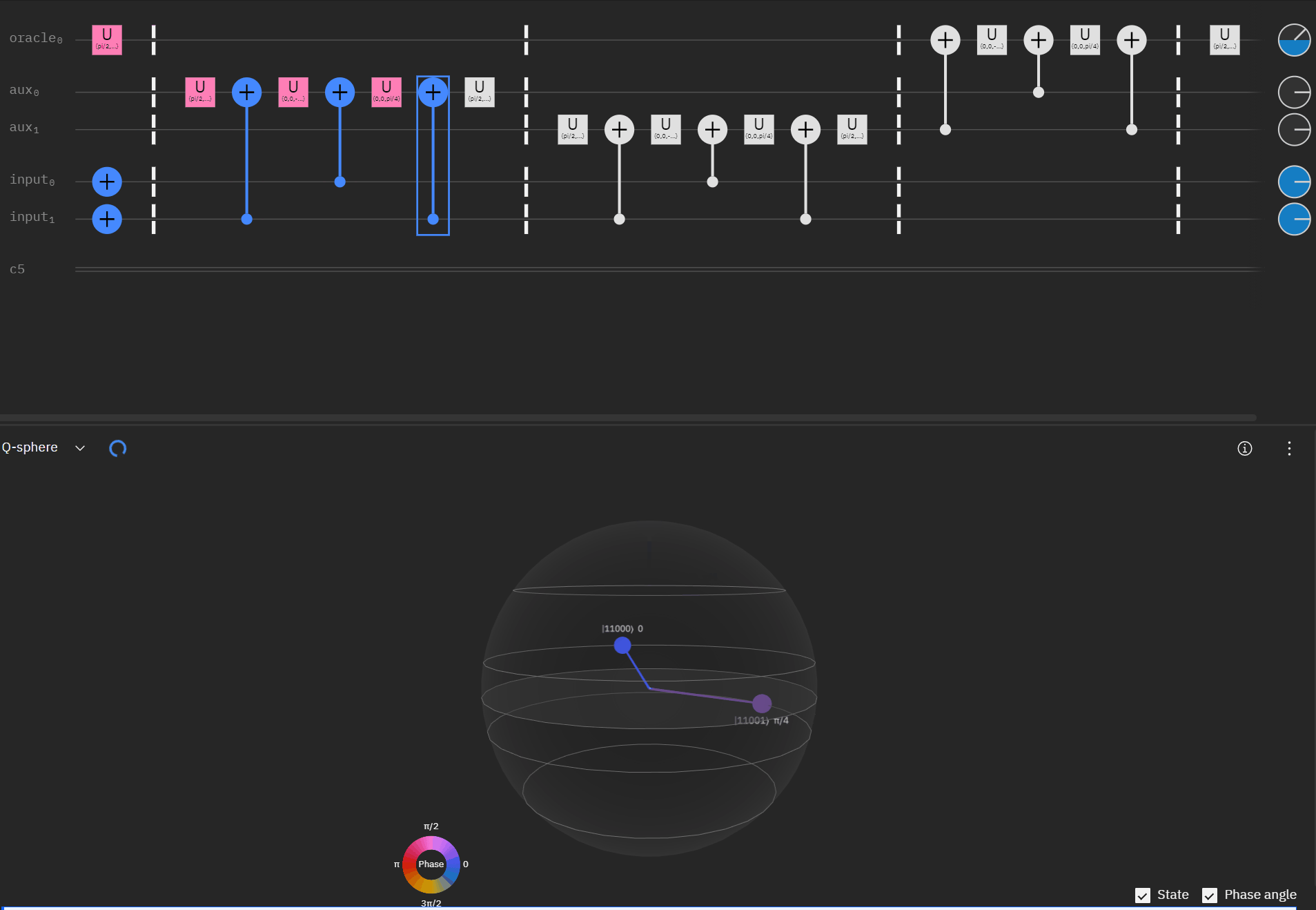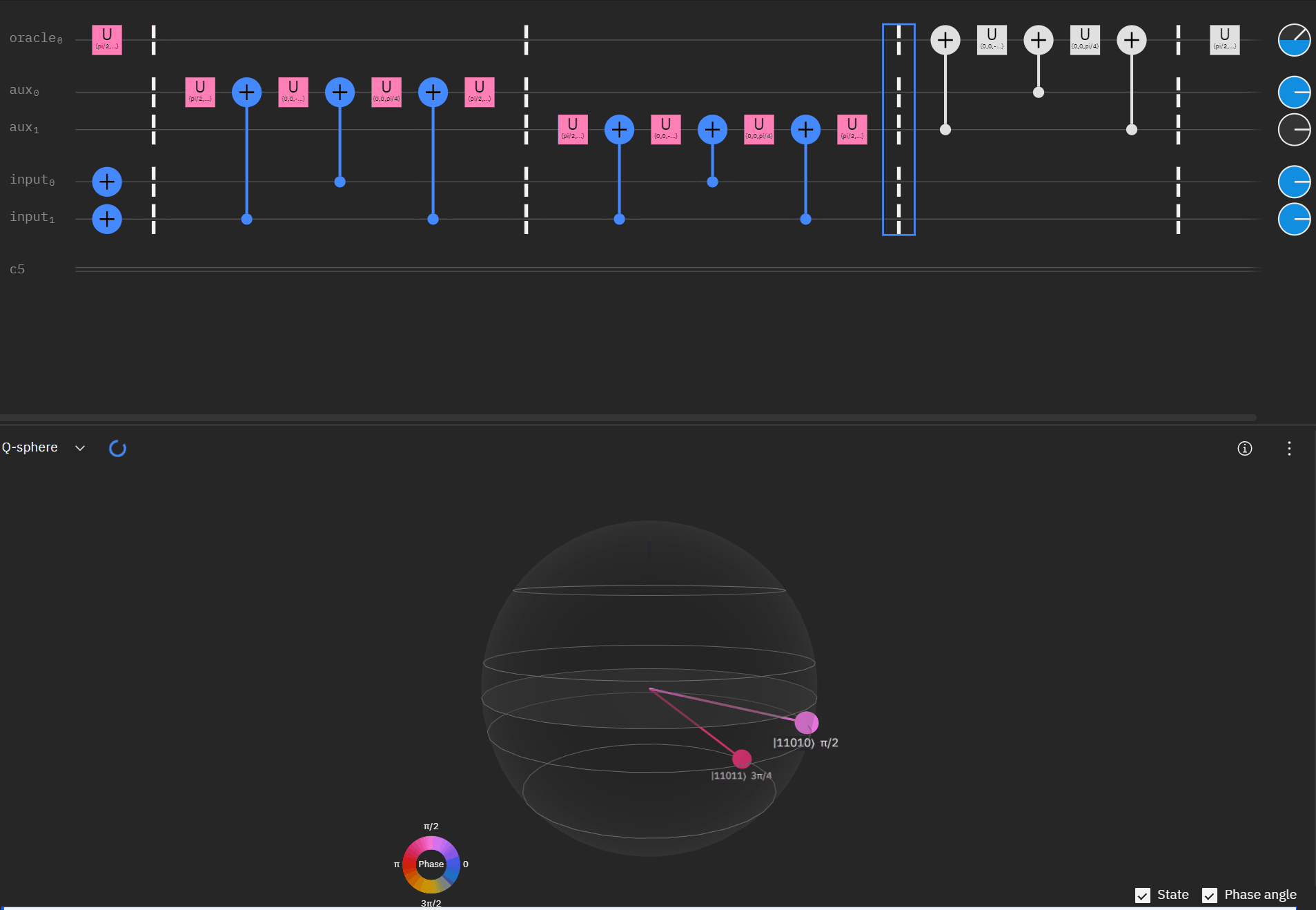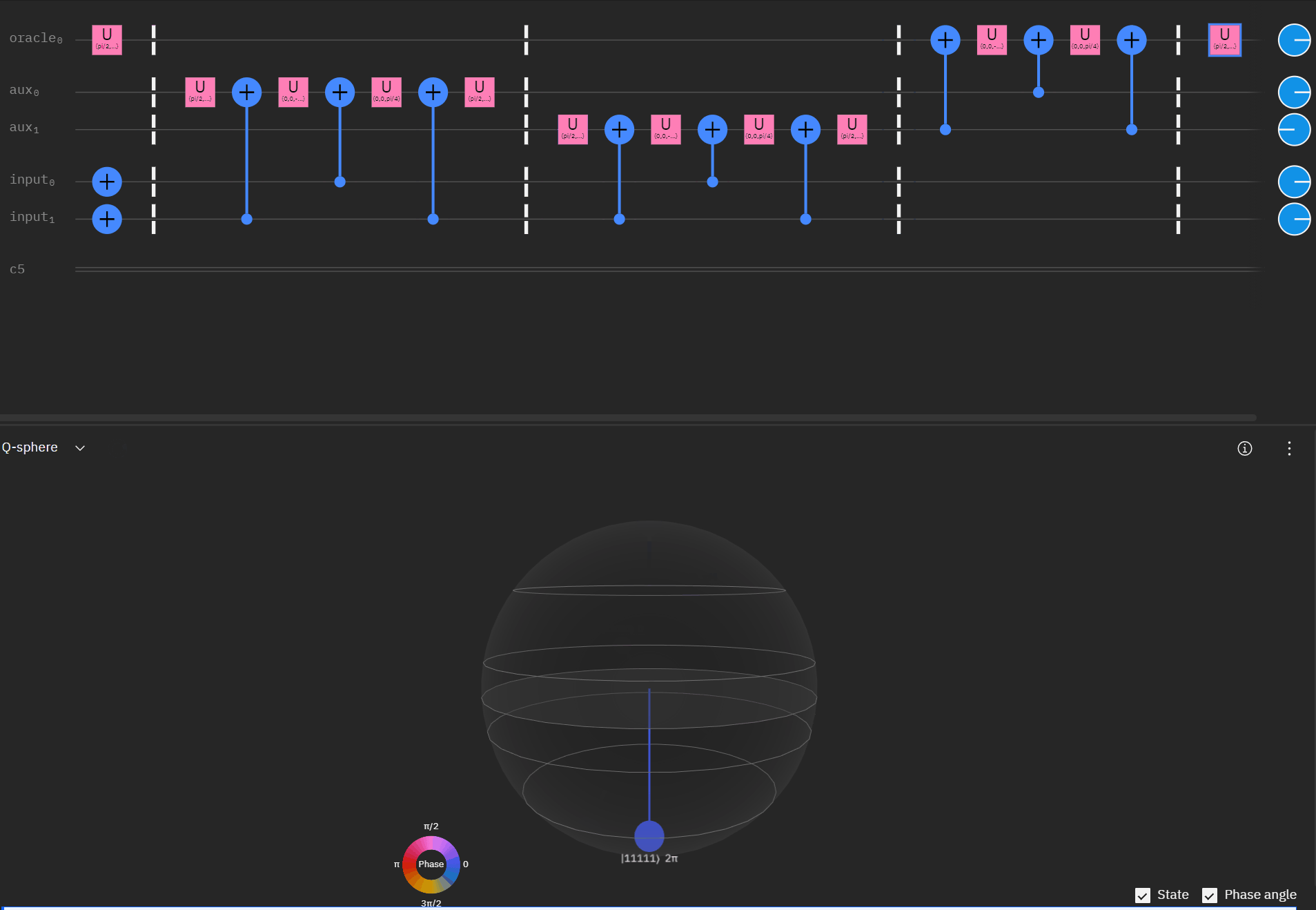
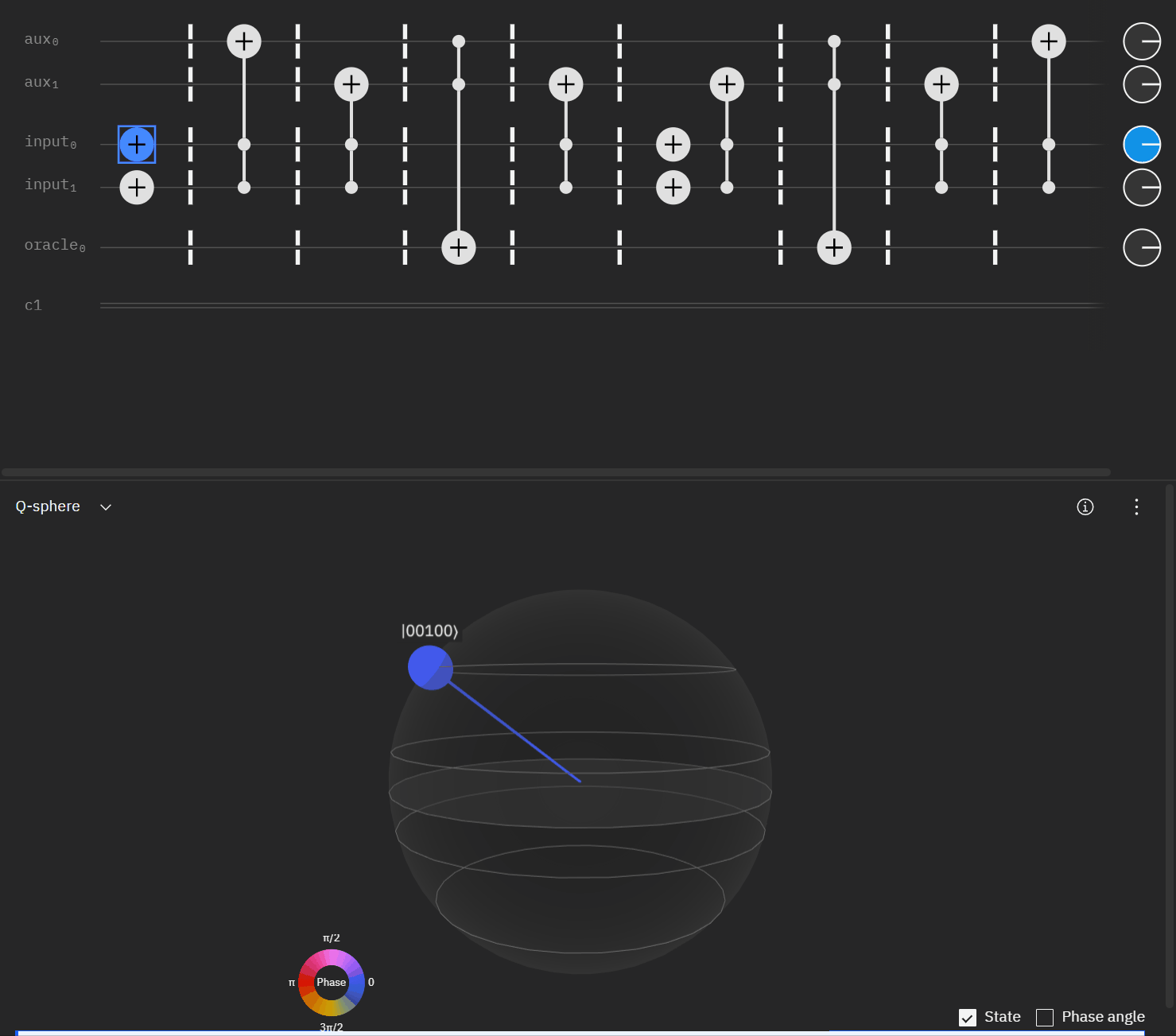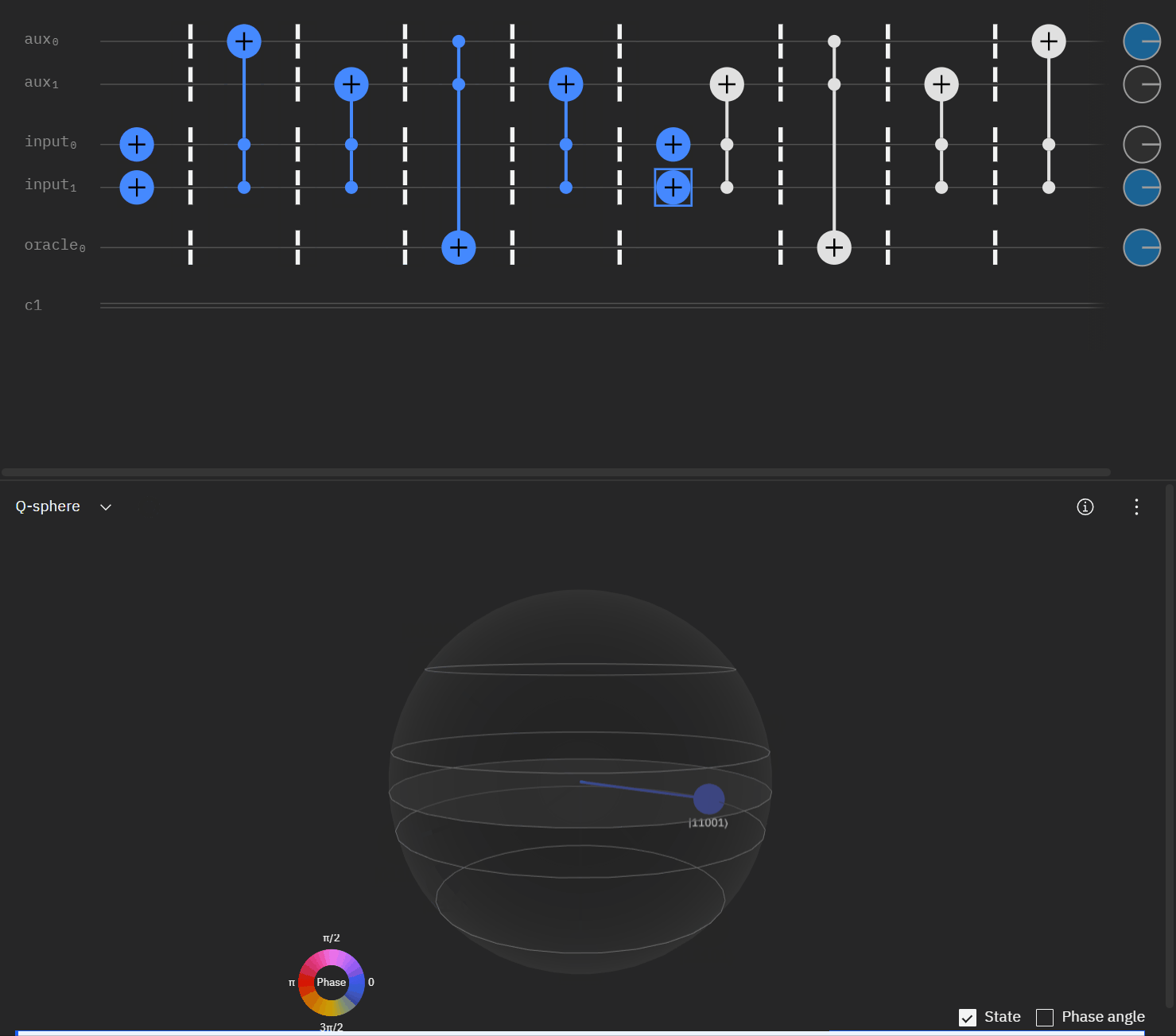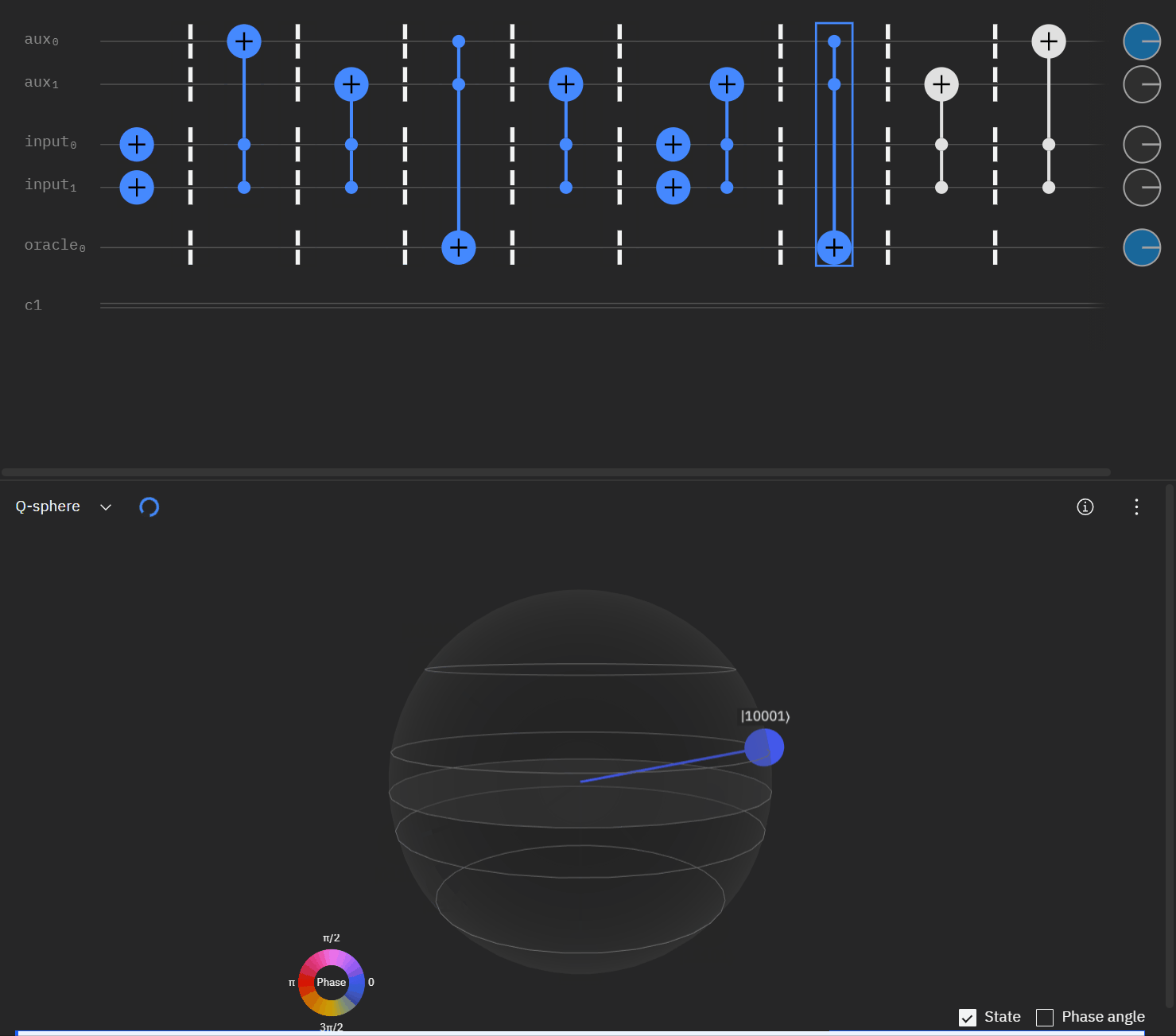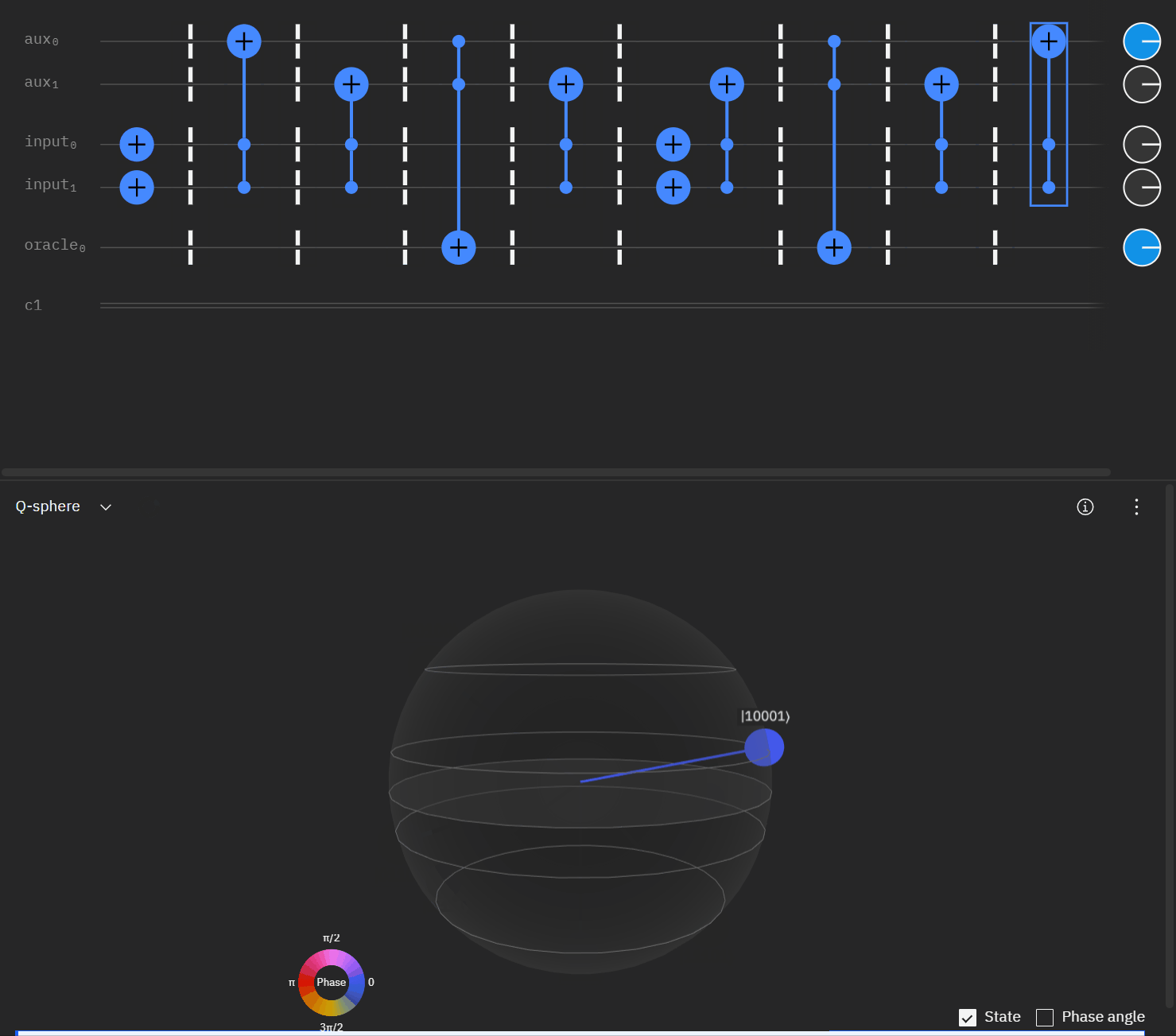
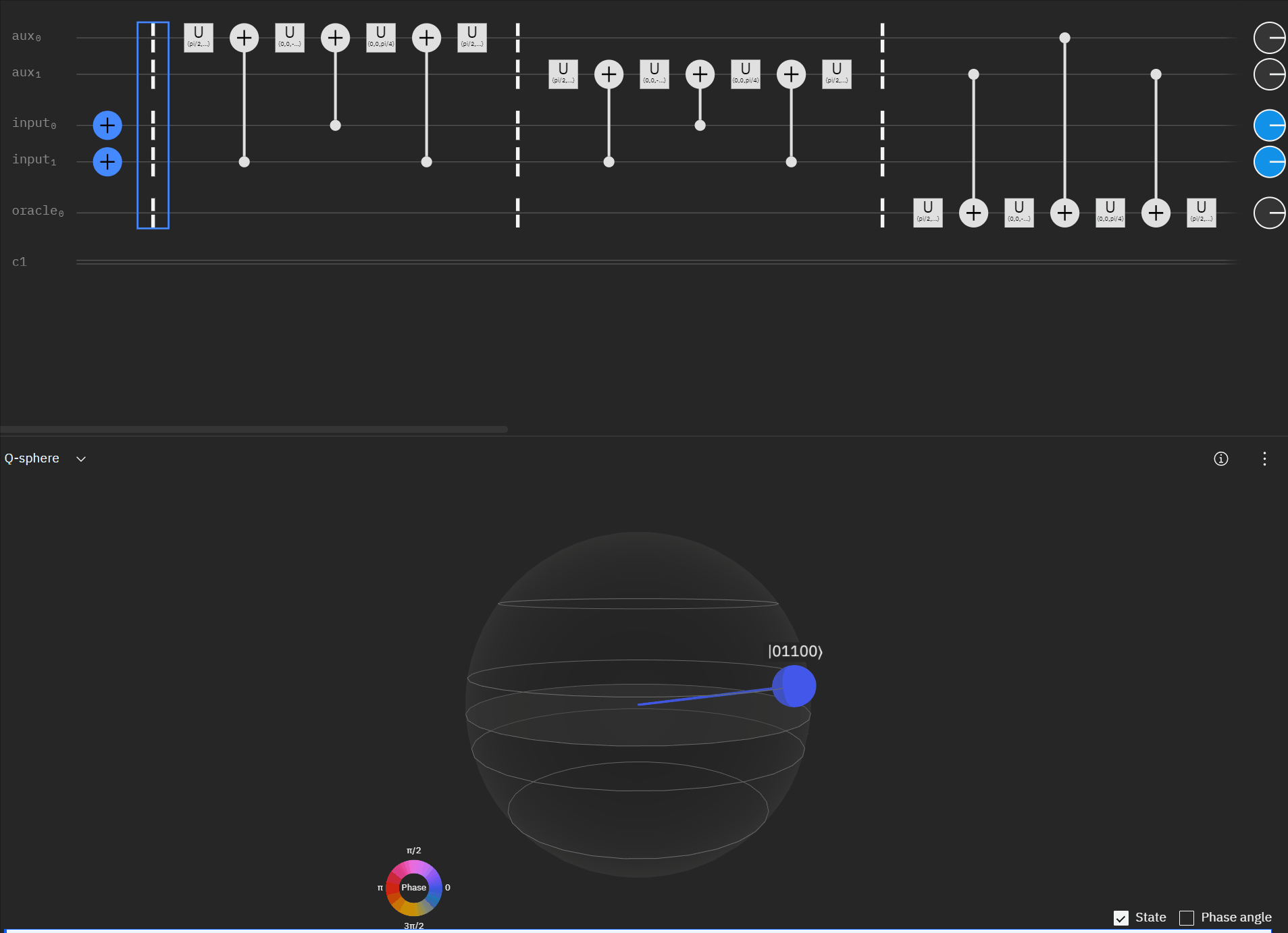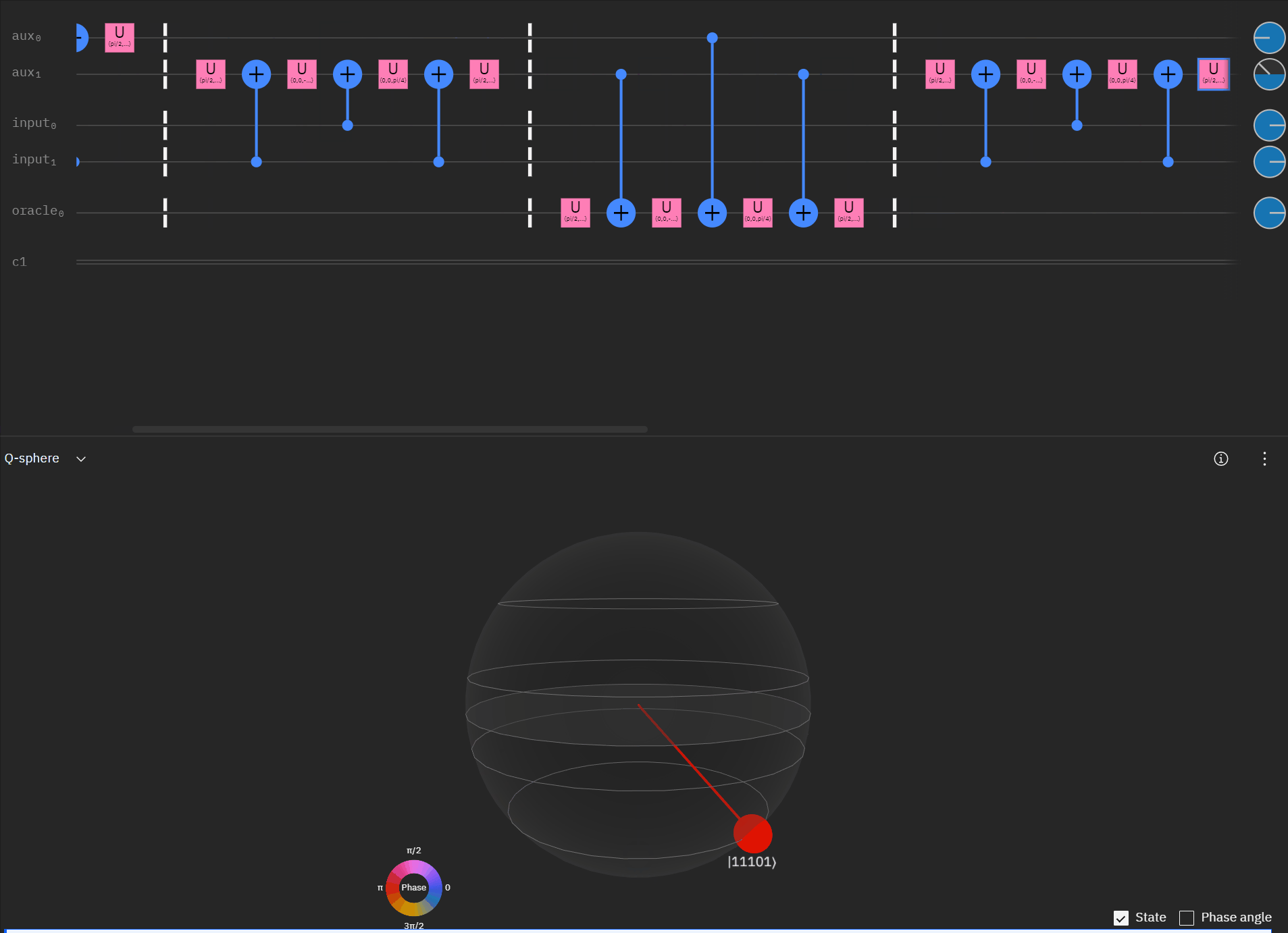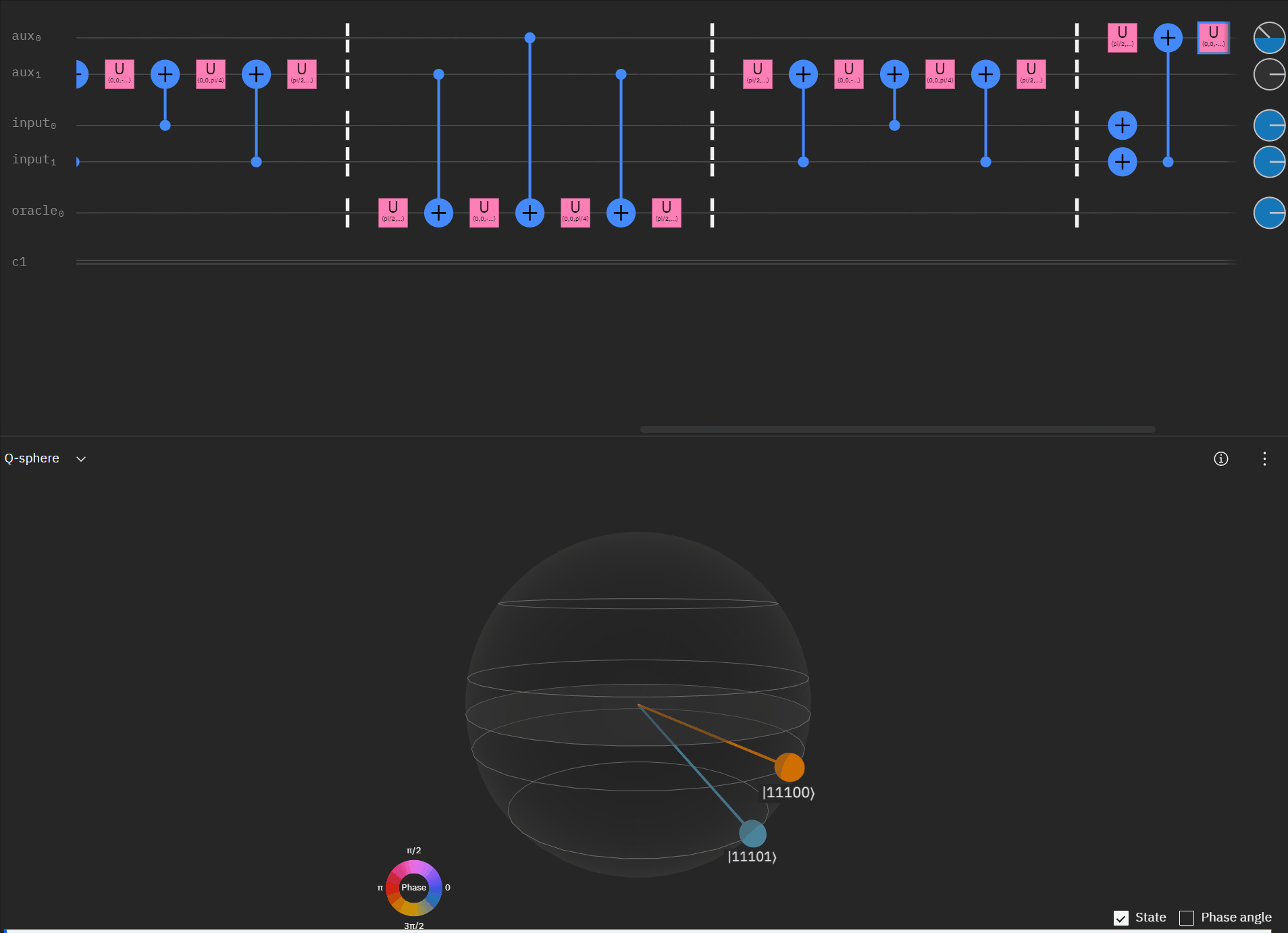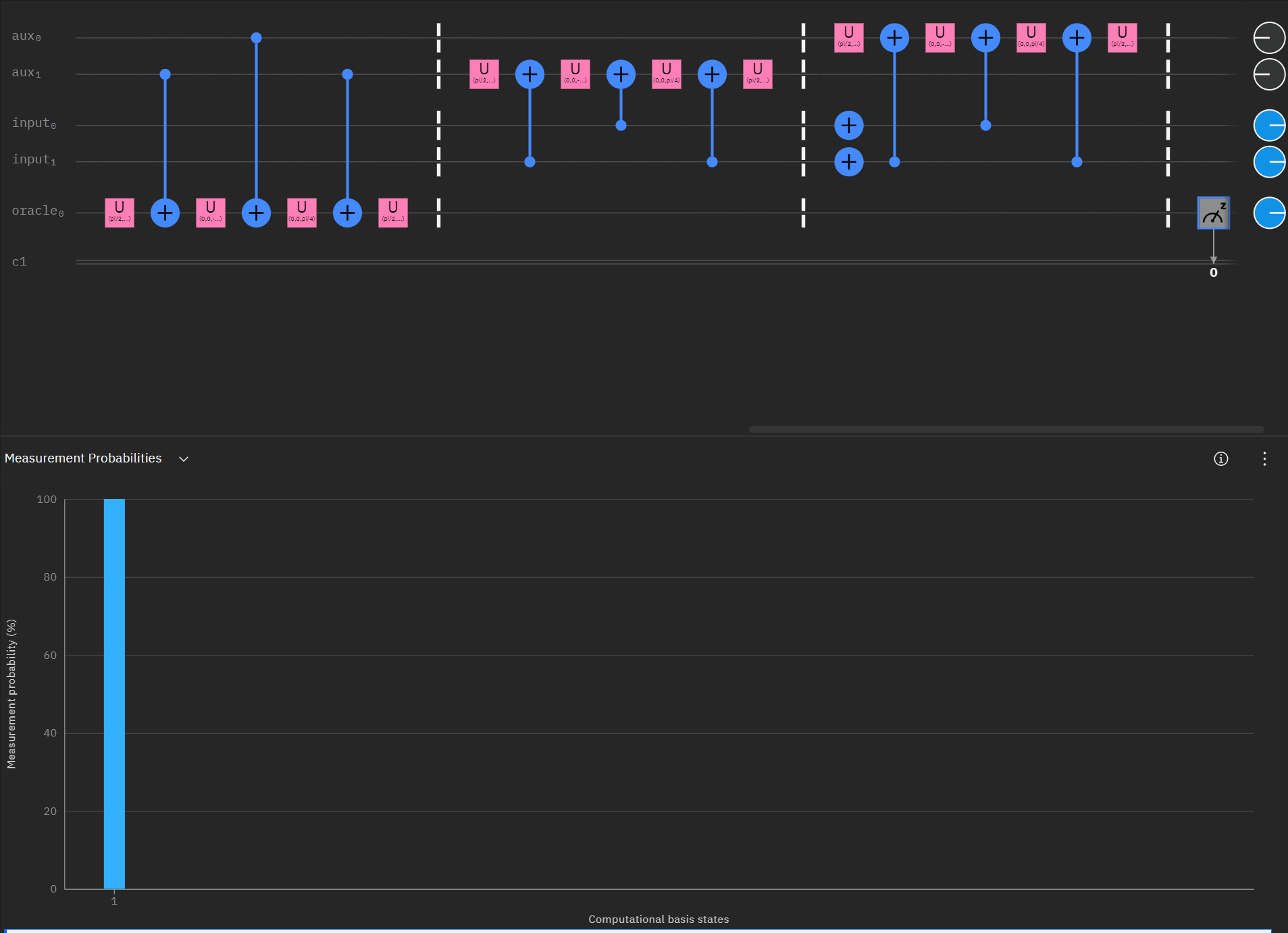
Although I couldn't directly use transpiler maybe I could tactically identify smaller components of my code, investigate what transpiler is doing to it in isolation, and see if I can adapt my overall circuit using that knowledge. The first part was to understand what is happening with a RCCX gate as this will form the basis of our work. Starting at this point I also used IBM's qSphere visualization to help understand in three dimensions what was going on. There were some limitations such as restricting the visual to 5 qubits or less that required me to be crafty in reusing "input" qubits, but I can honestly say I would probably not have gotten to where I ended up with without the visual aid.

Which translates to the following code:

# rotate aux0 and use 1st and 2nd items to flip aux0 if "on"
qc.u(pi/2,pi/4,pi,aux[0])
qc.cx(tile_qubits[det_clause[i][1]],aux[0])
qc.u(0,0,-pi/4,aux[0])
qc.cx(tile_qubits[det_clause[i][0]],aux[0])
qc.u(0,0,pi/4,aux[0])
qc.cx(tile_qubits[det_clause[i][1]],aux[0])
qc.u(pi/2,0,3*pi/4,aux[0])

Alright time to expand to a full "single oracle" iteration. Firstly let me mock up what I'm trying to solve.

Now working with the original RCCX/CCX example I can expand it to a full single oracle.

Where the code comes out to:

#rotate oracle for eventual matching check
qc.u(pi/2,pi/4,pi,oracle)

# rotate aux0 and use 1st and 2nd items to flip aux0 if "on"
qc.u(pi/2,pi/4,pi,aux[0])
qc.cx(tile_qubits[det_clause[i][1]],aux[0])
qc.u(0,0,-pi/4,aux[0])
qc.cx(tile_qubits[det_clause[i][0]],aux[0])
qc.u(0,0,pi/4,aux[0])
qc.cx(tile_qubits[det_clause[i][1]],aux[0])
qc.u(pi/2,0,3*pi/4,aux[0])

# rotate aux1 and use 3rd and 4th items to flip aux1 if "on"
qc.u(pi/2,pi/4,pi,aux[1])
qc.cx(tile_qubits[det_clause[i][3]],aux[1])
qc.u(0,0,-pi/4,aux[1])
qc.cx(tile_qubits[det_clause[i][2]],aux[1])
qc.u(0,0,pi/4,aux[1])
qc.cx(tile_qubits[det_clause[i][3]],aux[1])
qc.u(pi/2,0,3*pi/4,aux[1])

#At this point can be a winning clause if items 0,1,2,3 are on
#Which matches up to the first of two possibilities based on 0,1 items
# i.e. first det_clause = [0,5,10,15,11,14].
# If 0,5,10,15 are 1, it's a winning clause. At this point this is where it is checked

# check if both aux satisfy, then flip oracle
qc.cx(aux[1],oracle)
qc.u(0,0,-pi/4,oracle)
qc.cx(aux[0],oracle)
qc.u(0,0,pi/4,oracle)
qc.cx(aux[1],oracle)

So far so good! I had to tweak the rotation angles slightly as I proceeded to try and get back to an original phase. This is where the qSphere visual definitely helped keep track of where things were.

The last part to take into consideration is the "double oracle" approach where we are using the same first two qubits of the clause. Again let me mock up what I am doing with CCX/CX gates. Before anyone calls me out I did forget to reapply the X gates to input 1/2 during the second uncompute... but it theoretically shows what I was trying to achieve.

Now taking the single oracle circuit we added the second clause check in qSphere. Again with some slight angle adjustment where the visual helped.

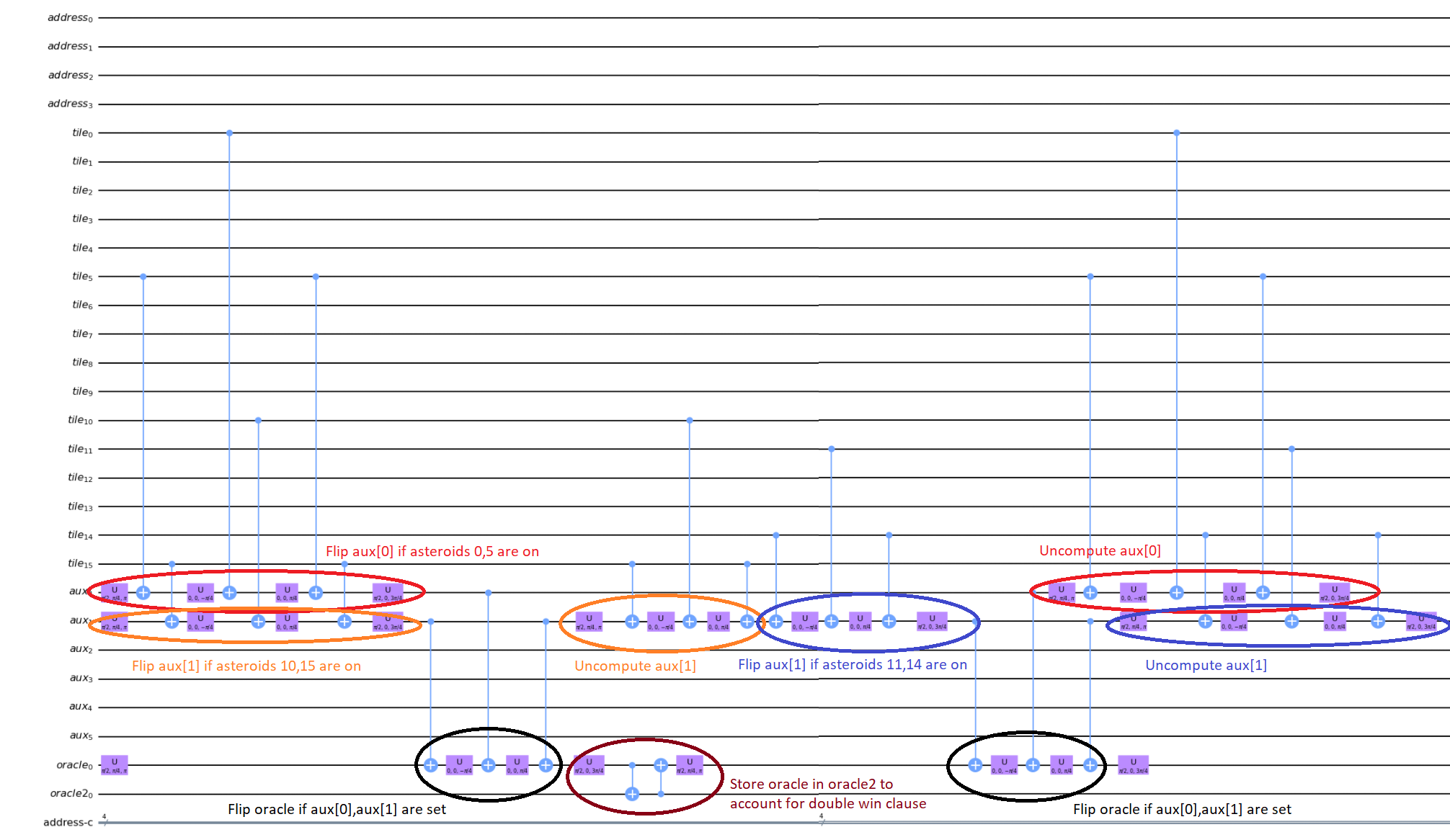
It may be easier for folks to follow the full circuit diagram below. Because of the qSpehere qubit limitations I had to omit above the oracle swap (double clause boards). I also added annotations to clarify a run through the first det_clause of [0,5,10,15,11,14].

The final oracle code ends up being:

#Prep rotate oracle for eventual matching check
qc.u(pi/2,pi/4,pi,oracle)

# rotate aux0 and use 1st and 2nd items to flip aux0 if "on"
qc.u(pi/2,pi/4,pi,aux[0])
qc.cx(tile_qubits[det_clause[i][1]],aux[0])
qc.u(0,0,-pi/4,aux[0])
qc.cx(tile_qubits[det_clause[i][0]],aux[0])
qc.u(0,0,pi/4,aux[0])
qc.cx(tile_qubits[det_clause[i][1]],aux[0])
qc.u(pi/2,0,3*pi/4,aux[0])

# rotate aux1 and use 3rd and 4th items to flip aux1 if "on"
qc.u(pi/2,pi/4,pi,aux[1])
qc.cx(tile_qubits[det_clause[i][3]],aux[1])
qc.u(0,0,-pi/4,aux[1])
qc.cx(tile_qubits[det_clause[i][2]],aux[1])
qc.u(0,0,pi/4,aux[1])
qc.cx(tile_qubits[det_clause[i][3]],aux[1])
qc.u(pi/2,0,3*pi/4,aux[1])

#At this point can be a winning clause if items 0,1,2,3 are on
#Which matches up to the first of two possibilities based on 0,1 items
# i.e. first det_clause = [0,5,10,15,11,14].
# If 0,5,10,15 are 1, it's a winning clause. At this point this is where it is checked

# check if both aux satisfy, then flip oracle
qc.cx(aux[1],oracle)
qc.u(0,0,-pi/4,oracle)
qc.cx(aux[0],oracle)
qc.u(0,0,pi/4,oracle)
qc.cx(aux[1],oracle)
#### ^ this is the final oracle flip if the first quatuplet of the clause matches
#swap oracle - accounting for double winning clause
# In reality should be rotating oracle before swapping
# however for the purposes of this problem, just swapping DOES return proper answers
# for all edge cases (double clause within the same first tuplet in det_clause)
# As there is no possibility for a double clause winner where one winner is
# the second quatuplet of det_clause & first quatuplet of the next det_clause
# because they always differ by 3 qubits, which cannot be represented by 6 asteroids.
# This fact allows us to swap oracle between the quatuplet pairs only instead of start
# of loop
qc.u(pi/2,0,3*pi/4,oracle)
qc.cx(oracle,oracle2)
qc.cx(oracle2,oracle)
#qc.cx(oracle,oracle2) ## is not required as we would only ever set oracle2 once at most
qc.u(pi/2,pi/4,pi,oracle)

## uncompute the 3rd and 4th clause winners to test the 5th and 6th (2nd quatuplet)
## unprepate aux[1] for the second set of checks. aux[0] doesn't change as it remains the same
qc.u(pi/2,pi/4,pi,aux[1])
# uncompute aux1 using 3rd/4th clause items
qc.cx(tile_qubits[det_clause[i][3]],aux[1])
qc.u(0,0,-pi/4,aux[1])
qc.cx(tile_qubits[det_clause[i][2]],aux[1])
qc.u(0,0,pi/4,aux[1])
qc.cx(tile_qubits[det_clause[i][3]],aux[1])
### start of second quatuplet check. compute aux1 if 5th/6th items are on
qc.cx(tile_qubits[det_clause[i][5]],aux[1])
qc.u(0,0,-pi/4,aux[1])
qc.cx(tile_qubits[det_clause[i][4]],aux[1])
qc.u(0,0,pi/4,aux[1])
qc.cx(tile_qubits[det_clause[i][5]],aux[1])
# prep aux1 and bring it back in line with aux0 for the check
qc.u(pi/2,0,3*pi/4,aux[1])

# Second oracle check. Now using the new aux[1]
# If both aux0,1 are on based on new phi angle, flip oracle
qc.cx(aux[1],oracle)
qc.u(0,0,-pi/4,oracle)
qc.cx(aux[0],oracle)
qc.u(0,0,pi/4,oracle)
qc.cx(aux[1],oracle)
# Now that both oracle checks are done, rotate oracle back, preserving "flip" if so
qc.u(pi/2,0,3*pi/4,oracle)

### time to clean up and uncompute previous steps - for both aux this time
# Start with aux0 
qc.u(pi/2,pi/4,pi,aux[0])
qc.cx(tile_qubits[det_clause[i][1]],aux[0])
qc.u(0,0,-pi/4,aux[0])
qc.cx(tile_qubits[det_clause[i][0]],aux[0])
qc.u(0,0,pi/4,aux[0])
qc.cx(tile_qubits[det_clause[i][1]],aux[0])
qc.u(pi/2,0,3*pi/4,aux[0])
# Uncompute aux1
qc.u(pi/2,pi/4,pi,aux[1])
qc.cx(tile_qubits[det_clause[i][5]],aux[1])
qc.u(0,0,-pi/4,aux[1])
qc.cx(tile_qubits[det_clause[i][4]],aux[1])
qc.u(0,0,pi/4,aux[1])
qc.cx(tile_qubits[det_clause[i][5]],aux[1])
qc.u(pi/2,0,3*pi/4,aux[1])

#### At this point both aux qubits are completely uncomputed and oracle is flipped
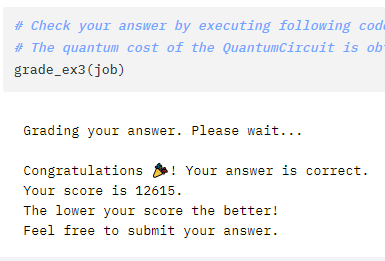
#### if either of the clauses are on. Preserved through rotation and oracle swap at the start

A submission later and I managed to get down to 12k as a result!

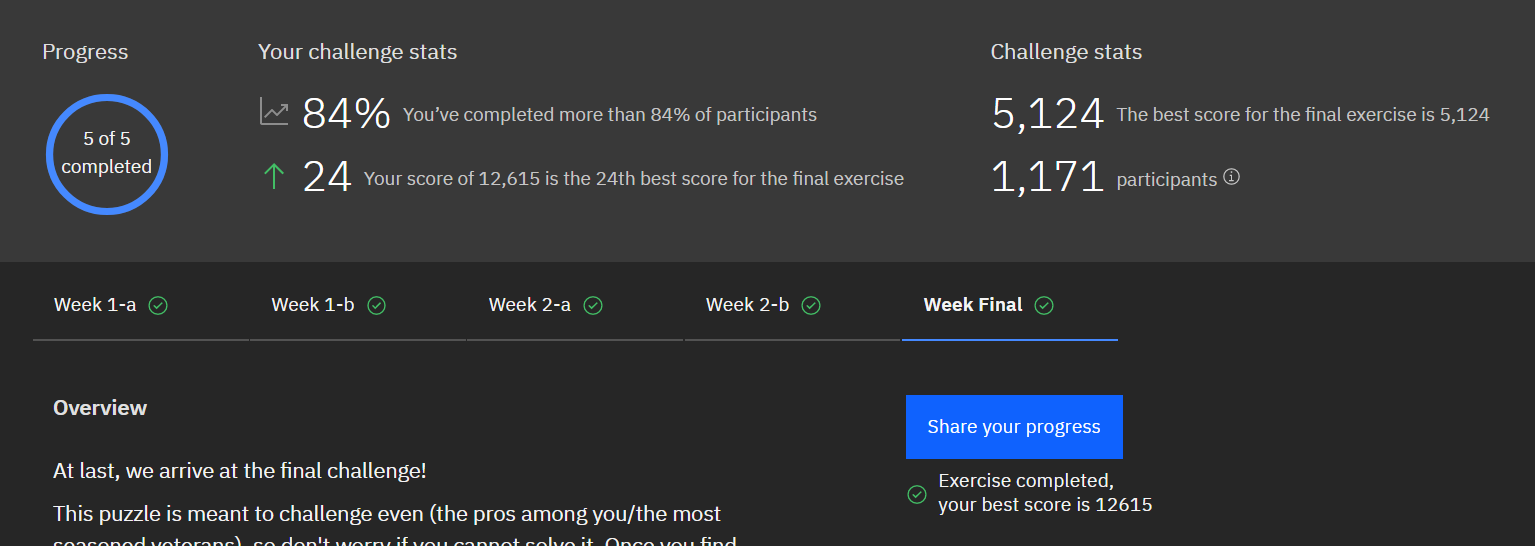
With that I was able to crack the top 25 submissions by close of the competition.

Conclusion & Recap

What a ride. When comparing this to IBM's May event it was almost a night and day difference in difficulty. With that came added time to truly deep dive and I appreciated the opportunity to spend time (trying) to understand more fundamentally than "make it work". With that said there were a few things that bothered me throughout the final challenge.

Firstly, I'm still not entirely sure if this was a coincidence or if there is a more fundamental reason as to why, but the careful observer might have noticed that I never initially set the negative phase to the two oracles. Regardless of if I set/unset the oracles phases (by using X/H gates) or did not, with a very small tweak I ended with same correct result, with different levels of amplification. I'd like to dig a bit deeper and understand if this was just a fluke, or if there some deeper meaning.

Secondly the issues and restrictions with the grader were frustrating. If the grader wasn't working properly that is one thing, technical issues happen. The more frustrating aspect was having to constantly doubt myself that my approach was "valid". I still don't fully know either! The rules were not necessarily clear, and the restrictions on what we could do and not do limited my willingness to be more creative in certain aspects.

Overall I really enjoyed the event. I learned a ridiculous amount over the three weeks! Even after the event closed I was still looking at my code and having discussions with other participants to continue that knowledge momentum. At the end of the day this is what it is all about - improving ourselves and pushing the envelop forward. Back in May I barely understood what was happening and managed to hobble through to completion. This time around, only a few months later, I understood enough to start diving into academic work and trying to apply it practically. I'm looking forward to dive deeper into certain topics I barely scraped the surface of and applying the new knowledge when the next Qiskit event rolls around!

For anyone who is interested I put up my challenge notebooks on my Github Repo.

Thanks folks, until next time!

Qiskit Quantum Challenge Fall 2020